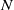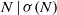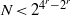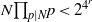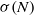Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Suzuki, Yuta
2018.
On amicable tuples.
Illinois Journal of Mathematics,
Vol. 62,
Issue. 1-4,
Vavilov, N. A.
2023.
Computers As a Novel Mathematical Reality: III. Mersenne Numbers and Sums of Divisors.
Doklady Mathematics,
Vol. 107,
Issue. 3,
p.
173.