Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T11:49:07.345Z Has data issue: false hasContentIssue false
  • English
  • Français

IDEMPOTENT RANK IN THE ENDOMORPHISM MONOID OF A NONUNIFORM PARTITION

Part of: Semigroups

Published online by Cambridge University Press:  10 August 2015

IGOR DOLINKA ,
JAMES EAST  and
JAMES D. MITCHELL
IGOR DOLINKA
Affiliation:
Department of Mathematics and Informatics, University of Novi Sad, Trg Dositeja Obradovića 4, 21101 Novi Sad, Serbia email [email protected]
JAMES EAST*
Affiliation:
Centre for Research in Mathematics, School of Computing, Engineering and Mathematics, University of Western Sydney, Locked Bag 1797, Penrith, NSW 2751, Australia email [email protected]
JAMES D. MITCHELL
Affiliation:
Mathematical Institute, School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife, KY16 9SS, UK email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

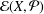We calculate the rank and idempotent rank of the semigroup ${\mathcal{E}}(X,{\mathcal{P}})$ generated by the idempotents of the semigroup 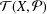${\mathcal{T}}(X,{\mathcal{P}})$ which consists of all transformations of the finite set 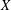$X$ preserving a nonuniform partition 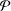${\mathcal{P}}$. We also classify and enumerate the idempotent generating sets of minimal possible size. This extends results of the first two authors in the uniform case.

Keywords

transformation semigroupsidempotentsgeneratorsrankidempotent rank

MSC classification

Primary: 20M20: Semigroups of transformations, etc.
Secondary: 20M17: Regular semigroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 1 , February 2016 , pp. 73 - 91
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Araújo, J., Bentz, W., Mitchell, J. D. and Schneider, C., ‘The rank of the semigroup of transformations stabilising a partition of a finite set’, Math. Proc. Cambridge Philos. Soc., to appear, arXiv:1404.1598.Google Scholar
Araújo, J. and Schneider, C., ‘The rank of the endomorphism monoid of a uniform partition’, Semigroup Forum 78(3) (2009), 498–510.CrossRefGoogle Scholar
Dolinka, I. and East, J., ‘Idempotent generation in the endomorphism monoid of a uniform partition’, Comm. Algebra, to appear, arXiv:1407.3312V2.Google Scholar
Gomes, G. and Howie, J. M., ‘On the ranks of certain finite semigroups of transformations’, Math. Proc. Cambridge Philos. Soc. 101(3) (1987), 395–403.CrossRefGoogle Scholar
Howie, J. M., ‘The subsemigroup generated by the idempotents of a full transformation semigroup’, J. Lond. Math. Soc. (2) 41 (1966), 707–716.CrossRefGoogle Scholar
Howie, J. M., ‘Idempotent generators in finite full transformation semigroups’, Proc. Roy. Soc. Edinburgh Sect. A 81(3–4) (1978), 317–323.CrossRefGoogle Scholar
Wright, E. M., ‘The number of irreducible tournaments’, Glasg. Math. J. 11 (1970), 97–101.CrossRefGoogle Scholar