Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lu, Jitan
1997.
Submanifolds whose quadric representations satisfy $\Delta\tilde{x}=B{\tilde{x}}+C$.
Kodai Mathematical Journal,
Vol. 20,
Issue. 2,
Lu, Jitan
1998.
Spherical submanifolds with special quadric representations.
Bulletin of the Australian Mathematical Society,
Vol. 57,
Issue. 2,
p.
295.


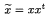 (where
(where 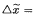
 , where
, where 