Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hou, Bo
2023.
Gerstenhaber algebra of ℤ2 × ℤ2-Galois covering of quantum exterior algebra.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 04,


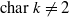 , and let Λ
, and let Λ