Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nese, Jon M.
1989.
Quantifying local predictability in phase space.
Physica D: Nonlinear Phenomena,
Vol. 35,
Issue. 1-2,
p.
237.
Kwon, Ern Gun
Lee, Jinkee
Kwon, Gun
and
Kim, Mi Hui
2019.
A Refinement of Schwarz–Pick Lemma for Higher Derivatives.
Mathematics,
Vol. 7,
Issue. 1,
p.
77.
Liu, Xiaosong
2023.
The Refined Schwarz-Pick Estimates for Positive Real Part Holomorphic Functions in Several Complex Variables.
Chinese Annals of Mathematics, Series B,
Vol. 44,
Issue. 2,
p.
265.


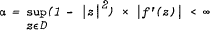 , with the expansion
, with the expansion 