Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T19:10:50.908Z Has data issue: false hasContentIssue false
  • English
  • Français

A HARMONIC SUM OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION

Part of: Zeta and $L$-functions: analytic theory Computational number theory

Published online by Cambridge University Press:  20 November 2020

RICHARD P. BRENT Open the ORCID record for RICHARD P. BRENT [Opens in a new window] ,
DAVID J. PLATT Open the ORCID record for DAVID J. PLATT [Opens in a new window]  and
TIMOTHY S. TRUDGIAN Open the ORCID record for TIMOTHY S. TRUDGIAN [Opens in a new window]
RICHARD P. BRENT
Affiliation:
Australian National University, Canberra, Australia e-mail: [email protected]
DAVID J. PLATT
Affiliation:
School of Mathematics, University of Bristol, Bristol, UK e-mail: [email protected]
TIMOTHY S. TRUDGIAN*
Affiliation:
School of Science, University of New South Wales, Canberra, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the sum 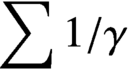$\sum 1/\gamma $ , where 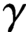$\gamma $ ranges over the ordinates of nontrivial zeros of the Riemann zeta-function in an interval 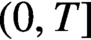$(0,T]$ , and examine its behaviour as 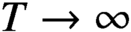$T \to \infty $ . We show that, after subtracting a smooth approximation 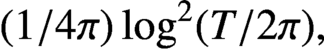$({1}/{4\pi }) \log ^2(T/2\pi ),$ the sum tends to a limit 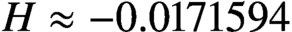$H \approx -0.0171594$ , which can be expressed as an integral. We calculate H to high accuracy, using a method which has error 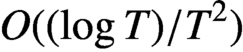$O((\log T)/T^2)$ . Our results improve on earlier results by Hassani [‘Explicit approximation of the sums over the imaginary part of the non-trivial zeros of the Riemann zeta function’, Appl. Math. E-Notes16 (2016), 109–116] and other authors.

Keywords

accelerationnontrivial zerosRiemann zeta-function

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11Y60: Evaluation of constants
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 59 - 65
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author is supported by ARC Grants DP160100932 and FT160100094; the second author is supported by ARC Grant DP160100932 and EPSRC Grant EP/K034383/1.

References

Brent, R. P. and Johansson, F., ‘A bound for the error term in the Brent–McMillan algorithm’, Math. Comp. 84(295) (2015), 2351–2359.CrossRefGoogle Scholar
Brent, R. P. and McMillan, E. M., ‘Some new algorithms for high-precision computation of Euler’s constant’, Math. Comp. 34(149) (1980), 305–312.Google Scholar
Brent, R. P., Platt, D. J. and Trudgian, T. S., ‘The mean square of the error term in the prime number theorem’, Preprint, 2020, arXiv:2008.06140v1.Google Scholar
Büthe, J., ‘Estimating $\pi (x)$ and related functions under partial RH assumptions’, Math. Comp. 85(301) (2016), 2483–2498.CrossRefGoogle Scholar
Demailly, J.-P., ‘Precise error estimate of the Brent–McMillan algorithm for the computation of Euler’s constant’, Mosc. J. Comb. Number Theory 7(4) (2017), 271–306.Google Scholar
Fujii, A., ‘On the zeros of the Riemann zeta function’, Comment. Math. Univ. St. Pauli 51(1) (2002), 1–17.Google Scholar
Hassani, M., ‘Explicit approximation of the sums over the imaginary part of the non-trivial zeros of the Riemann zeta function’, Appl. Math. E-Notes 16 (2016), 109–116.Google Scholar
Lehman, R. S., ‘On the difference $\pi (x)-\mathrm{li}(x)$ ’, Acta Arith. 11 (1966), 397–410.CrossRefGoogle Scholar
Odlyzko, A. M., ‘On the distribution of spacings between zeros of the zeta function’, Math. Comp. 48(177) (1987), 273–308.CrossRefGoogle Scholar
Saouter, Y., Trudgian, T. and Demichel, P., ‘A still sharper region where $\pi (x)-\mathrm{li}(x)$ is positive’, Math. Comp. 84(295) (2015), 2433–2446.CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (ed. Heath-Brown, D. R.) (Oxford University Press, Oxford, 1986).Google Scholar
Trudgian, T. S., ‘Improvements to Turing’s method’, Math. Comp. 80(276) (2011), 2259–2279.CrossRefGoogle Scholar
Trudgian, T. S., ‘An improved upper bound for the argument of the Riemann zeta-function on the critical line II’, J. Number Theory 134 (2014), 280–292.CrossRefGoogle Scholar