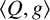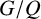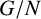GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP

Abstract

A group is called quasihamiltonian if all its subgroups are permutable, and we say that a subgroup Q of a group G is permutably embedded in G if $\langle Q,g\rangle $ is quasihamiltonian for each element g of G. It is proved here that if a group G contains a permutably embedded normal subgroup Q such that $G/Q$ is Černikov, then G has a quasihamiltonian subgroup of finite index; moreover, if G is periodic, then it contains a Černikov normal subgroup N such that $G/N$ is quasihamiltonian. This result should be compared with theorems of Černikov and Schlette stating that if a group G is Černikov over its centre, then G is abelian-by-finite and its commutator subgroup is Černikov.

1 Introduction

A classical theorem of Schur [14] states that if the centre $\zeta (G)$ of a group G has finite index, then the commutator subgroup $G'$ is finite. Several results of Schur type were later proved by replacing the finiteness of the index $|G:\zeta (G)|$ with a suitable restriction on the factor group $G/\zeta (G)$ . It is known for instance that if G is a group such that $G/\zeta (G)$ is Černikov, then also $G'$ is a Černikov group, that is, an abelian-by-finite group satisfying the minimal condition on subgroups. This latter result has been often, and erroneously, attributed to Polovickiı̆ (see for instance [6, 8] and [10, Part 1, Theorem 4.23]); actually, it was due to Černikov [1], and Polovickiı̆ himself wrote in [9]: ‘This proposition is easily obtained from our Lemma 1, in view of the result proved in [1] which states the extremality of the commutator subgroup of any central extension by an extremal group’. A proof of Černikov’s theorem can also be found in a paper of Schlette [12], where she also proved that if G is a group such that $G/\zeta (G)$ is Černikov, then G is abelian-by-finite.

A different approach to Schur’s theorem was adopted in [2] by replacing the centre by a normal subgroup with a suitable embedding property. Obviously, a subgroup C of a group G is contained in $\zeta (G)$ if and only if $\langle g,C\rangle $ is abelian for all $g\in G$ , and we say that a subgroup Q is permutably embedded in G if $\langle g,Q\rangle $ is quasihamiltonian for all $g\in G$ ; here a group is called quasihamiltonian if $XY=YX$ for all its subgroups X and Y. It was proved in [2] that if a group G contains a permutably embedded subgroup of finite index, then there exists a finite normal subgroup N of G such that the factor group $G/N$ is quasihamiltonian.

The aim of this paper is to look at groups which are Černikov over a permutably embedded normal subgroup and so our first main result should be compared with the above quoted theorem of Schlette; recall here that a group is Černikov if and only if it contains a subgroup of finite index which is the direct product of finitely many Prüfer subgroups.

Theorem 1.1. Let G be a group containing a permutably embedded normal subgroup Q such that $G/Q$ is a Černikov group and let $J/Q$ be the largest divisible subgroup of $G/Q$ . Then J is quasihamiltonian and, in particular, G is quasihamiltonian-by-finite.

Our second main result shows that in the periodic case, a satisfactory translation of Černikov’s theorem in terms of permutability holds.

Theorem 1.2. Let G be a periodic group containing a permutably embedded normal subgroup Q such that $G/Q$ is a Černikov group. Then G has a Černikov normal subgroup N such that $G/N$ is quasihamiltonian.

Our notation is mostly standard and can be found in [10].

2 Preliminaries

A modular lattice $\mathfrak {L }$ is called permodular if for all elements a and b of $\mathfrak {L}$ such that $b\leq a$ , the interval $[a/b]=\{ x\in \mathfrak {L}\;|\; b\leq x\leq a\}$ is finite whenever it has finite length. Moreover, if G is a group and $\mathfrak {L}(G)$ is the lattice of all subgroups of G, a modular element M of $\mathfrak {L}(G)$ is said to be permodular in G if the index $|\langle M,g\rangle :Y|$ is finite for all elements g and for all subgroups Y of G such that $M\leq Y\leq \langle M,g\rangle $ and the interval $[\langle M,g\rangle /Y]$ is finite. Since cyclic subgroups and subgroups of finite index can be detected within the lattice of subgroups, permodular subgroups are recognisable by means of purely lattice theoretic concepts. Actually, it is known that a group has a permodular subgroup lattice if and only if all its subgroups are permodular (see [13, Theorem 6.4.3]). Notice here that every finite modular lattice is obviously permodular, but, for instance, the subgroup lattice of a Tarski group (that is, an infinite simple group whose proper nontrivial subgroups have prime order) is modular but not permodular.

Recall also that a subgroup X of a group G is said to be permutable in G if $XY=YX$ for all subgroups Y of G. Thus, a group is quasihamiltonian if and only if all its subgroups are permutable. Since a subgroup is permutable if and only if it is modular and ascendant (see for instance [13, Theorem 6.2.10]), it follows that a group is quasihamiltonian if and only if it is locally nilpotent and its subgroup lattice is modular. Thus, the study of periodic quasihamiltonian groups reduces to that of primary quasihamiltonian groups, and these latter are known to be either abelian or nilpotent of finite exponent (see [13, Theorem 2.4.14]). The structure of nonperiodic quasihamiltonian groups is described by the following result (see [13, Theorem 2.4.11]); it shows in particular that the commutator subgroup of any quasihamiltonian group is locally finite.

Lemma 2.1. Let G be a quasihamiltonian group which is neither periodic nor abelian. Then the subgroup T of all elements of finite order of G is abelian and the torsion-free group $G/T$ is locally cyclic. Moreover, all subgroups of T are normal in G and each element of G whose order is either a prime or $4$ belongs to $\zeta (G)$ .

We refer to the monograph [13, Chs. 5 and 6] for further results concerning the behaviour of permutable and permodular subgroups of infinite groups that can be useful for our considerations. We only note here that if Q is a permutably embedded subgroup of a group G, then Q is permutable in G and quasihamiltonian.

3 Proof of Theorem 1.1

Let G be a group and let X be a subgroup of G. We say that the interval $[G/X]$ of $\mathfrak {L}(G)$ is Černikov if it satisfies the minimal condition and there exists a permodular subgroup P of G containing X such that the index $|G:P|$ is finite and the lattice $[P/X]$ is permodular. Since periodic groups with a permodular subgroup lattice are locally finite (see [13, Theorem 2.4.16]) and locally finite groups satisfying the minimal condition are Černikov groups by an important theorem of Šunkov (see for instance [4, Theorem 1.6.15]), a group G is Černikov if and only if $\mathfrak {L}(G)=[G/\{1\}]$ is a Černikov lattice.

It is well known that a group is locally cyclic if and only if it has a distributive subgroup lattice (see [13, Theorem 1.2.3]), and so our first lemma may be considered as a translation of the elementary fact that a group G is abelian when the factor group $G/\zeta (G)$ is locally cyclic.

Lemma 3.1. Let G be a group containing a permutably embedded subgroup Q such that the interval $[G/Q]$ is a distributive lattice. Then G is quasihamiltonian.

Proof. Let E be any finitely generated subgroup of G. Then

$$ \begin{align*}[E/E\cap Q]\simeq[\langle E,Q\rangle/Q]\end{align*} $$

is a distributive lattice, and so, in particular, the finitely generated group $E/(E\cap Q)^E$ is cyclic. Moreover, the index $|(E\cap Q)^E:E\cap Q|$ is finite because $E\cap Q$ is permutable in G (see [13, Lemma 6.2.8]). Thus, the lattice $[E/E\cap Q]$ satisfies the maximal condition so that there exists an element x such that $E=\langle x,E\cap Q\rangle $ (see [3, Corollary 2.4]) and hence E is quasihamiltonian. Since the property of being quasihamiltonian is local, it follows that G is also a quasihamiltonian group.

Lemma 3.2. Let G be a group and let N be a periodic normal subgroup of G. If N is contained in the hypercentre of G and $G/C_G(N)$ has no proper subgroups of finite index, then $N\leq \zeta (G)$ .

Proof. Assume for a contradiction that N is not contained in $\zeta (G)$ so that $N\cap \zeta (G)$ is a proper subgroup of $N\cap \zeta _2(G)$ . Consider an element a of $\bigl (N\cap \zeta _2(G)\bigr )\setminus \zeta (G)$ and let k be the order of a. Since the map $g\mapsto [a,g]$ is an epimorphism from G onto $[a,G]$ with kernel $C_G(a)$ , the nontrivial subgroup $[a,G]$ is a homomorphic image of $G/C_G(N)$ , which is impossible because $[a,G]^k=[a^k,G]=\{1\}$ .

Lemma 3.3. Let G be a group containing a permutably embedded nonperiodic subgroup Q such that the interval $[G/Q]$ is a Černikov lattice. Then the elements of finite order of G form a locally finite subgroup T containing $G'$ and $Q\cap T\leq \zeta (T)$ . Moreover, all periodic subgroups of Q are normal in G and each element of Q whose order is either a prime or $4$ belongs to $\zeta (G)$ .

Proof. By Schlette’s result, we may suppose that Q is not contained in $\zeta (G)$ so that there is a $g\in G$ such that $[Q,g]\neq \{1\}$ . Since the subgroup $\langle g,Q\rangle $ is quasihamiltonian, it follows from Lemma 2.1 that Q has torsion-free rank $1$ . Let E be any finitely generated subgroup of G and put $X=\langle Q,E\rangle $ and $Y=Q^X$ . Then $X/Y$ is finitely generated and $\mathfrak {L}(X/Y)$ is a Černikov lattice so that $X/Y$ is finite. Moreover, the index $|Y:Q|$ is finite (see [13, Lemma 6.2.8]) and hence Q has finite index in X. It follows now from [2, Theorem 3.5] that X contains a finite normal subgroup L such that $X/L$ is quasihamiltonian. Thus, $X'$ is locally finite so the arbitrary choice of E yields that $G'$ is locally finite and hence the elements of finite order of G form a locally finite subgroup T containing $G'$ . If x is any element of T, the nonperiodic subgroup $\langle x,Q\rangle $ is quasihamiltonian so that $\langle x,Q\cap T\rangle $ is abelian by Lemma 2.1 and hence $Q\cap T\leq \zeta (T)$ .

Let a be any element of infinite order of G. Then $\langle a,Q\rangle $ is quasihamiltonian so that a normalises all subgroups of $Q\cap T$ and centralises each element of Q which has order either a prime or $4$ (see [13, Theorem 2.4.11]). Since G is generated by its elements of infinite order, the proof is complete.

Proof of Theorem 1.1

Since $G/Q$ is Černikov, the subgroup J has finite index in G and so it is enough to prove that J is quasihamiltonian. Thus without loss of generality, we may assume that $G/Q$ is a direct product of $r\geq 1$ Prüfer subgroups. Suppose first $r=1$ so that $G/Q$ is a group of type $q^\infty $ for some prime number q and hence the subgroup lattice of $G/Q$ is distributive. In this case, the group G is quasihamiltonian by Lemma 3.1. Assume now $r>1$ . Let p be any prime in the set $\pi =\pi (G/Q)$ and $P/Q$ any subgroup of type $p^\infty $ of $G/Q$ . Thus,

$$ \begin{align*}G/Q=P/Q\times V/Q,\end{align*} $$

where $V/Q$ is the direct product of $r-1$ Prüfer subgroups so that P is quasihamiltonian by the first part of the proof, while V is quasihamiltonian by induction on r. In particular, P and V are hypercentral and hence $G=PV$ is also a hypercentral group (see [10, Part 1, page 51]).

Suppose that G is periodic and write $P=P_1\times P_2$ , where $P_1$ is a p-subgroup and $P_2$ is a $p'$ -subgroup. Since $P_1$ has infinite exponent, it is abelian (see [13, Theorem 2.4.14]) and so $P_1\leq \zeta (P)$ . Thus, $Q\leq C_G(P_1)$ and hence $G/C_G(P_1)$ is divisible. Application of Lemma 3.2 yields that $P_1$ is contained in $\zeta (G)$ . It follows that the largest $\pi $ -subgroup $O_\pi (G)$ of G lies in $\zeta (G)$ . However, the largest $\pi '$ -subgroup $O_{\pi '}(G)$ of G is contained in Q and hence $G=O_\pi (G)\times O_{\pi '}(G)$ is quasihamiltonian.

Assume finally that G is not periodic so that Q is not periodic. It follows from Lemma 3.3 that $G'$ is locally finite, whence the elements of finite order of G form a locally finite subgroup T and $G'\leq Q\cap T\leq \zeta (T)$ . Let x be any element of T and put $C=C_G(x)$ . Then $G'\leq C$ and so C is normal in G. Since $\langle x,Q\rangle $ is a nonperiodic quasihamiltonian group, the subgroup $\langle x\rangle $ is normalised by Q so that $N_G(\langle x\rangle )$ is normal in G and $G/N_G(\langle x\rangle )$ is a Černikov group. It follows that $G/C$ is also Černikov. If $R/C$ is the largest divisible subgroup of $G/C$ , Lemma 3.2 yields that R centralises x and so x has only finitely many conjugates in G. Thus, $G/C$ is finite so that $G=QC$ and $\langle x\rangle $ is normal in G. Moreover, by Lemma 2.1, $[x,Q]=\{1\}$ whenever the order of x is a prime or $4$ and so $[x,G]=\{1\}$ under the same assumption. Therefore the group G is quasihamiltonian (see [13, Theorem 2.4.11]) and the proof is complete.

4 Proof of Theorem 1.2

The first result of this section is an elementary lemma concerning divisible homomorphic images of abelian groups.

Lemma 4.1. Let A be an abelian group and let B be a subgroup of A of finite exponent e. If $A/B$ is divisible, then $A^e$ is the largest divisible subgroup of A. Moreover, if $A/B$ is a group of type $p^\infty $ for some prime number p, then $A^e$ is also of type $p^\infty $ .

Proof. The map $a\longmapsto a^e$ defines an epimorphism of A onto $A^e$ whose kernel contains B so that $A^e$ is divisible and hence $A=A^e\times C$ for a suitable subgroup C. Obviously, C has finite exponent and so $A^e$ is the largest divisible subgroup of A. If $A/B$ is a group of type $p^\infty $ for some prime p, then $A^e$ is also of type $p^\infty $ since it is a nontrivial homomorphic image of $A/B$ .

Lemma 4.2. Let G be a periodic group and let Q be a permutably embedded p-subgroup of G, where p is a prime number. Then Q is contained in $\zeta _k(G)$ for some nonnegative integer k.

Proof. Of course, it can be assumed that $[Q,g]\neq \{1\}$ for a suitable element g of G. Since the subgroup $\langle Q,g\rangle $ is quasihamiltonian, it follows from [13, Theorem 2.4.14] that Q has finite exponent e. Let x be an element of Q of order p and let y be an arbitrary element of G. Then $\langle y\rangle $ is a permutable subgroup of $\langle Q,y\rangle $ and so, in particular, $\langle y\rangle ^x=\langle y\rangle $ . Thus, x normalises all subgroups of G and hence it belongs to $\zeta _2(G)$ (see for instance [11]). Therefore, $Q\zeta _2(G)/\zeta _2(G)$ has exponent strictly smaller than e and so by induction Q is contained in some term of the upper central series of G with finite ordinal type.

Corollary 4.3. Let G be a periodic group and let Q be a permutably embedded subgroup of G. Then Q is contained in $\zeta _\omega (G)$ .

Proof. Each primary subgroup of Q is permutably embedded in G and so by Lemma 4.2, it is contained in some term with finite ordinal type of the upper central series of G. Therefore, $Q\leq \zeta _\omega (G)$ .

In relation to the above statement, we notice that a permutably embedded subgroup Q of a periodic group G need not be contained in some term with finite ordinal type of the upper central series of G, even if $[G/Q]$ is a Černikov lattice. To see this, it is enough to observe that for each prime p, there exists a quasihamiltonian p-group $G_p$ of class p and consider the direct product $G=\mathop {\textrm {Dr}}_pG_p$ , which is quasihamiltonian but not nilpotent. However, it can be proved that if a permutably embedded subgroup Q of a periodic group G determines a Černikov interval of $\mathfrak {L}(G)$ , then it is always subnormal in G and it lies in some term with finite ordinal type of the upper central series of G provided that it is core-free. To see this, we need the following result.

Lemma 4.4. Let G be a periodic locally nilpotent group and let X be a subgroup of G such that the interval $[G/X]$ is a Černikov lattice. Then X contains all but finitely many Sylow subgroups of G.

Proof. Let $p_1<p_2<\cdots <p_n<p_{n+1}<\cdots $ be the sequence of all prime numbers. For each positive integer n, let $P_n$ be the unique Sylow $p_n$ -subgroup of G and put $G_n=\mathop {\textrm {Dr}}_{k\geq n}P_k$ . Then,

$$ \begin{align*}G=G_1=XG_1\geq XG_2\geq\cdots\geq XG_n\geq XG_{n+1}\geq\cdots\end{align*} $$

is a descending sequence of subgroups of G containing X and so there exists m such that $XG_n=XG_{n+1}$ for all $n\geq m$ . If $X_n$ is the unique Sylow $p_n$ -subgroup of X, we have $[X_n,G_{n+1}]=\{1\}$ so that $X_n$ is normal in $XG_{n+1}$ and $XG_{n+1}/X_n$ has no elements of order $p_n$ . Thus, $P_n=X_n\leq X$ for all $n\geq m$ and hence $G_m$ is contained in X.

Theorem 4.5. Let G be a periodic group and let Q be a permutably embedded subgroup of G such that the interval $[G/Q]$ is a Černikov lattice. Then $Q/Q_G$ is contained in $\zeta _k(G/Q_G)$ for some nonnegative integer k. In particular, Q is subnormal in G.

Proof. By Corollary 4.3, the subgroup Q is contained in $Z=\zeta _\omega (G)$ . Thus, the subgroup lattice of $G/Z$ is Černikov and so $G/Z$ is a Černikov group. Let $J/Z$ be the largest divisible subgroup of $G/Z$ . Then $G/J$ is finite and J is hypercentral so that it follows from Lemma 4.4 that there exists a finite set $\pi $ of prime numbers such that $\pi (G/J)\subseteq \pi $ and Q contains the $\pi '$ -component $J_{\pi '}$ of J. Then $Q_{\pi '}=J_{\pi '}$ is normal in G and $G/Q_{\pi '}$ is a $\pi $ -group. Application of Lemma 4.2 to each primary component of $Q/Q_{\pi '}$ yields that $Q/Q_{\pi '}\leq \zeta _k(G/Q_{\pi '})$ for a suitable nonnegative integer k, and hence $Q/Q_G$ lies in $\zeta _k(G/Q_G)$ .

Proof of Theorem 1.2

The subgroup Q is contained in $\zeta _\omega (G)$ by Corollary 4.3 so that $G/\zeta _\omega (G)$ is a Černikov group and hence there exists a Černikov normal subgroup W of G such that $G/W$ is hypercentral (see [5, Corollary B4]). Since the hypotheses are inherited by homomorphic images, we may replace G by $G/W$ and assume that G is hypercentral. In particular, G is the direct product of its Sylow subgroups. Put $\pi =\pi (G/Q)$ . Then the largest $\pi '$ -subgroup $G_{\pi '}$ of G is contained in Q and hence it is quasihamiltonian. Clearly, the set $\pi $ is finite and $G=G_\pi \times G_{\pi '}$ so that it is enough to prove that the statement is true for every Sylow subgroup of G. Thus, we may suppose that G is a p-group for some prime number p.

Since Q is quasihamiltonian, it is abelian-by-finite (see [13, Theorem 2.4.14]) and so it contains an abelian characteristic subgroup A of finite index (see for instance [7, Lemma 21.1.4]). Then A is a permutably embedded normal subgroup of G and $G/A$ is Černikov so that Q can be replaced by A and we may assume that Q is abelian. Moreover, by the results of Černikov and Schlette, we may also suppose that Q is not contained in $\zeta (G)$ . Thus there exists $g\in G$ such that $\langle g,Q\rangle $ is a nonabelian quasihamiltonian group, whence Q must have finite exponent. It follows from Lemma 4.2 that $Q\leq \zeta _k(G)$ for some nonnegative integer k so that the factor group $G/\zeta _k(G)$ is Černikov. Therefore, $\gamma _{k+1}(G)$ is also a Černikov group (see [10, Part 1, Corollary 2 to Theorem 4.21]) and hence it is enough to prove the statement for the factor group $G/\gamma _{k+1}(G)$ . Thus, we may assume without loss of generality that G is nilpotent.

Let $J/Q$ be the largest divisible subgroup of the Černikov group $G/Q$ . Then Q is contained in $\zeta (J)$ by Lemma 3.2 so that $J'$ is Černikov, and again we may replace G by $G/J'$ and assume that J is abelian. Write

$$ \begin{align*}J/Q=J_1/Q\times\cdots\times J_t/Q,\end{align*} $$

where each $J_i/Q$ is a group of type $p^\infty $ . It follows from Lemma 4.1 that $J_i=P_i\times B_i$ , where $P_i$ is a group of type $p^\infty $ and $B_i$ has finite exponent i ( $i=1,\ldots ,t$ ). Since G is nilpotent, $J/Q$ lies in $\zeta (G/Q)$ so that each $J_i$ is normal in G and hence also $P_i$ is normal in G for every $i=1,\ldots ,t$ . It follows that $P=\langle P_1,\ldots ,P_t\rangle $ is a Černikov normal subgroup of G. Moreover, $J/P$ has finite exponent and so $J=PQ$ . Therefore, $J/P$ is a permutably embedded subgroup of finite index of $G/P$ and hence $G/P$ contains a finite normal subgroup $N/P$ such that $G/N$ is quasihamiltonian (see [2, Theorem 3.5]). Since N is Černikov, the proof is complete.