Article contents
Generating groups of nilpotent varieties
Published online by Cambridge University Press: 17 April 2009
Abstract
If 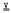 is a variety of groups which are nilpotent of class c then
is a variety of groups which are nilpotent of class c then 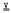 is generated by its free group of rank c. It is proved that under certain general conditions
is generated by its free group of rank c. It is proved that under certain general conditions 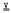 cannot be generated by its free group of rank c - 2, and that under certain other conditions
cannot be generated by its free group of rank c - 2, and that under certain other conditions 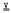 is generated by its free group of rank c - 1. It follows from these results that if
is generated by its free group of rank c - 1. It follows from these results that if 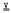 is the variety of all groups which are nilpotent of class c, then the least value of k such that the free group of
is the variety of all groups which are nilpotent of class c, then the least value of k such that the free group of 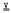 of rank k generates
of rank k generates 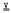 is c - 1. This extends known results of L.G. Kovács, M.F. Newman, P.P. Pentony (1969) and F. Levin (1970).
is c - 1. This extends known results of L.G. Kovács, M.F. Newman, P.P. Pentony (1969) and F. Levin (1970).
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1970
References
- 7
- Cited by


