Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T08:21:07.422Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS

Part of: Graph theory Abelian groups Representation theory of groups

Published online by Cambridge University Press:  29 January 2019

CRISTINA ACCIARRI Open the ORCID record for CRISTINA ACCIARRI [Opens in a new window]  and
ANDREA LUCCHINI Open the ORCID record for ANDREA LUCCHINI [Opens in a new window]
CRISTINA ACCIARRI
Affiliation:
Department of Mathematics, University of Brasilia, 70910-900 Brasília DF, Brazil email [email protected]
ANDREA LUCCHINI*
Affiliation:
Università degli Studi di Padova, Dipartimento di Matematica ‘Tullio Levi-Civita’, Via Trieste 63, 35121 Padova, Italy email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a group 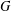$G$, let 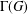$\unicode[STIX]{x1D6E4}(G)$ denote the graph defined on the elements of 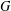$G$ in such a way that two distinct vertices are connected by an edge if and only if they generate 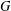$G$. Let 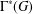$\unicode[STIX]{x1D6E4}^{\ast }(G)$ be the subgraph of 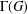$\unicode[STIX]{x1D6E4}(G)$ that is induced by all the vertices of 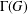$\unicode[STIX]{x1D6E4}(G)$ that are not isolated. We prove that if 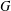$G$ is a 2-generated noncyclic abelian group, then 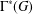$\unicode[STIX]{x1D6E4}^{\ast }(G)$ is connected. Moreover, 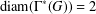$\text{diam}(\unicode[STIX]{x1D6E4}^{\ast }(G))=2$ if the torsion subgroup of 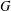$G$ is nontrivial and 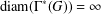$\text{diam}(\unicode[STIX]{x1D6E4}^{\ast }(G))=\infty$ otherwise. If 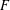$F$ is the free group of rank 2, then 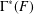$\unicode[STIX]{x1D6E4}^{\ast }(F)$ is connected and we deduce from 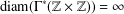$\text{diam}(\unicode[STIX]{x1D6E4}^{\ast }(\mathbb{Z}\times \mathbb{Z}))=\infty$ that 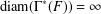$\text{diam}(\unicode[STIX]{x1D6E4}^{\ast }(F))=\infty$.

Keywords

abelian groupsgenerationgenerating graphfree groupsFibonacci numbers

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 20K15: Torsion-free groups, finite rank
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 68 - 75
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

Research partially supported by MIUR-Italy via PRIN ‘Group theory and applications’. The first author is also supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico CNPq-Brazil and FAPDF.

References

Carter, D. and Keller, G., ‘Elementary expressions for unimodular matrices’, Comm. Algebra 12(3–4) (1984), 379–389.Google Scholar
Crestani, E. and Lucchini, A., ‘The generating graph of finite soluble groups’, Israel J. Math. 198(1) (2013), 63–74.Google Scholar
Lazard, D., ‘Le meilleur algorithme d’Euclide pour K[X] et ℤ’, C. R. Acad. Sci. Paris Sér. A–B 284(1) (1977), A1–A4.Google Scholar
Lucchini, A., ‘The diameter of the generating graph of a finite soluble group’, J. Algebra 492 (2017), 28–43.Google Scholar
Magnus, W., Karrass, A. and Solitar, D., Combinatorial Group Theory, reprint of the 1976 second edition (Dover, Mineola, NY, 2004).Google Scholar
O’Meara, O. T., ‘On the finite generation of linear groups over Hasse domains’, J. reine angew. Math. 217 (1965), 79–108.Google Scholar