Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T20:10:46.369Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of a theorem of Aquaro

Published online by Cambridge University Press:  17 April 2009

C.E. Aull
C.E. Aull
Affiliation:
Department of Mathematics, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

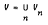In this paper we introduce the concept of a δθ-cover to generalize Aquaro's Theorem that every point countable open cover of a topological space such that every discrete closed family of sets is countable has a countable subcover. A δθ-cover of a space X is defined to be a family of open sets where each Vn covers X and for x є X there exists n such that Vn is of countable order at x. We replace point countable open cover by a δθ-cover in Aquaro's Theorem and also generalize the result of Worrell and Wicke that a θ-refinable countably compact space is compact and Jones′ result that ℵ1-compact Moore space is Lindelöf which was used to prove his classic result that a normal separable Moore space is metrizable, using the continuum hypothesis.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 9 , Issue 1 , August 1973 , pp. 105 - 108
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Aquaro, G., “Point countable open coverings in countably compact spaces”, General topology and its relations to modern analysis and algebra. II, 39–41 (Proc. 2nd Prague Topological Symposium, 1966; Academia [Publishing House of the Czechoslovak Academy of Sciences], Prague, 1967).CrossRefGoogle Scholar
[2]Arens, Richard and Dugundji, J., “Remark on the concept of compactness”, Portugal. Math. 9 (1950), 141–143.Google Scholar
[3]Boyte, J.M., “A note on compactness and metacompactness”, Proc. Japan Acad. 46 (1970), 1084–1085.CrossRefGoogle Scholar
[4]Burke, Dennis K., “On p–spaces and wΔ-spaces”, Pacific J. Math. 35 (1970), 285–296.CrossRefGoogle Scholar
[5]Christian, U.J., “Concerning certain minimal cover refinable spaces”, Fund. Math. 76 (1972), 213–222.CrossRefGoogle Scholar
[6]Jones, F.B., “Concerning normal and completely normal spaces”, Bull. Amer. Math. Soc. 43 (1937), 671–677.CrossRefGoogle Scholar
[7]Moore, R.L., Foundations of point set theory (Colloquium Publ. 13. Amer. Math. Soc., Providence, Rhode Island, 1962).Google Scholar
[8]Worrell, J.M. Jr and Wicke, H.H., “Characterizations of developable topological spaces”, Canad. J. Math. 17 (1965), 820–830.CrossRefGoogle Scholar