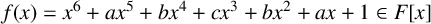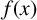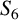GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS

Abstract

Let F be a subfield of the complex numbers and $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$ an irreducible polynomial. We give an elementary characterisation of the Galois group of $f(x)$ as a transitive subgroup of $S_6$. The method involves determining whether three expressions involving a, b and c are perfect squares in F and whether a related quartic polynomial has a linear factor. As an application, we produce one-parameter families of reciprocal sextic polynomials with a specified Galois group.

1 Introduction

Let F be a subfield of the complex numbers and $f(x)\in F[x]$ an irreducible polynomial of degree n. Identifying the Galois group, $\operatorname {\mathrm {Gal}}(f)$ , of $f(x)$ as a transitive subgroup of $S_n$ is a fundamental problem in computational algebra. In general, this is a difficult task; most modern approaches are based on [9, 10]. However, when $f(x)$ has a special form, the computation can be more straightforward.

For example, Galois groups of even quartic polynomials ( $x^4+ax^2+b$ ), even sextic polynomials ( $x^6+ax^4+bx^2+c$ ) and doubly even octic polynomials ( $x^8+ax^4+b$ ) have elementary characterisations (see for example [1, 2]). In each case, the characterisation leverages information about the index-2 subfield of the field defined by the polynomial.

A natural extension of this technique is to irreducible reciprocal polynomials, which are polynomials satisfying $f(x) = x^n\cdot f(1/x)$ , since the field extension defined by such a polynomial also has an index-2 subfield (see Theorem 2.1). Note that if $f(x) = \sum _{i=0}^n f_i x^i$ is a reciprocal polynomial, then $f_i = f_{n-i}$ ; that is, the sequence of coefficients $\{f_i\}$ forms a palindrome.

In this setting, some similar characterisations of $\operatorname {\mathrm {Gal}}(f)$ are known. The following classical result of Dickson determines the Galois group of an irreducible reciprocal quartic polynomial by testing the squareness of two elements of F (see [4]). In the theorem, as in the rest of the paper, we will use the following standard convention for describing groups: $C_n$ denotes the cyclic group of order n, $D_n$ the dihedral group of order $2n$ , and $A_n$ and $S_n$ the alternating and symmetric groups on n letters, respectively. We also use $\times $ to denote a direct product, $\rtimes $ a semidirect product and $\wr $ a wreath product.

Theorem 1.1 (Dickson)

Let $x^4+ax^3+bx^2+ax+1 \in F[x]$ be irreducible. Then $\operatorname {\mathrm {Gal}}(f)$ is isomorphic to:

• • $C_2\times C_2$ if and only if $(b+2)^2-4a^2$ is a square in F;

• • $C_4$ if and only if $((b+2)^2-4a^2)(a^2-4b+8)$ is a square in F;

• • $D_4$ if and only if neither $(b+2)^2-4a^2$ nor $((b+2)^2-4a^2)(a^2-4b+8)$ is a square in F.

Since reciprocal polynomials of odd degree are reducible (they have $-1$ as a root), the next logical case to consider is Galois groups of irreducible reciprocal sextic polynomials; that is, those of the form $x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$ . The purpose of this paper is to provide a similar characterisation, reflecting the spirit of Theorem 1.1. In doing so, we will generalise the results in [6, 7], which verify that certain families of irreducible reciprocal sextic polynomials with rational coefficients have Galois group isomorphic to either $S_3$ , $D_6$ or $S_4\times C_2$ .

The remainder of the paper is organised as follows. In Section 2, we collect several results concerning field extensions defined by reciprocal polynomials and their Galois groups; these will be used to prove our main theorem in Section 3. Our main result, Theorem 3.5, gives a characterisation of the Galois group of $x^6+ax^5+bx^4+cx^3+bx^2+ax+1$ that depends only on the squareness of three elements whose expressions involve a, b and c, along with whether or not a related quartic polynomial has a linear factor. As an application, we provide one-parameter families of reciprocal sextics for each possible Galois group (see Theorem 3.7).

2 Preliminary results

In this section, we let $f(x) \in F[x]$ be a monic irreducible reciprocal polynomial of degree $n=2m$ , and we let $L = F(\alpha )$ where $f(\alpha )=0$ . We collect results about L and $\operatorname {\mathrm {Gal}}(f)$ that are used later in the paper.

The reader is referred to [8] for an elementary overview of several standard facts about reciprocal polynomials. One such result shows there exists a polynomial $g(x)$ of degree m such that $f(x) = x^m\cdot g(x+1/x)$ (see [8, Proposition 2.0.16]). It turns out that $g(x)$ is the minimal polynomial of $\alpha +1/\alpha $ . This result is straightforward to establish and shows L has an index-2 subfield. For convenience, we include a proof.

Theorem 2.1. The minimal polynomial, $g(x)$ , of $\beta = \alpha +1/\alpha $ has degree m. Thus, L has a subfield, $K=F(\beta )$ , of index 2.

Proof. Let the roots of $f(x)$ be $\{\alpha = r_1, 1/r_1, \ldots , r_m, 1/r_m\}$ , and let $g(x)$ be the polynomial whose roots are $\{r_i+1/r_i\}$ for $1\leq i\leq m$ . Thus, the degree of $g(x)$ is m and $g(\beta )=0$ . Let $h(x) = x^m\cdot g(x+1/x)$ . It follows that $f(x) = h(x)$ since both polynomials are monic, are of the same degree and have the same roots. If $g(x)$ were reducible, say $g(x) = k(x)\cdot l(x)$ , then this would imply $f(x)$ is reducible since

$$ \begin{align*} f(x) = h(x) = x^{\text{deg}(k)} k(x+1/x) \cdot x^{\text{deg}(l)} l(x+1/x).\end{align*} $$

However, this contradicts the irreducibility of $f(x)$ . Thus, $g(x)$ is irreducible and is therefore the minimal polynomial of $\beta $ .

Since subfields of L correspond to block systems of $\operatorname {\mathrm {Gal}}(f)$ (see [5, Section 1.6] for more information about block systems), it follows that $\operatorname {\mathrm {Gal}}(f)$ can be embedded in a suitable wreath product. In particular, the following is an immediate consequence of Theorem 2.1 and [5, Theorem 2.6 A].

Corollary 2.2. We have $\operatorname {\mathrm {Gal}}(f)$ is a subgroup of $C_2 \wr \operatorname {\mathrm {Gal}}(g) \simeq C_2^m \rtimes \operatorname {\mathrm {Gal}}(g)$ . Thus, $2^m \cdot m!$ is an upper bound for $|\kern-1.5pt\operatorname {\mathrm {Gal}}(f)|$ .

3 Galois groups of reciprocal sextics

For the rest of the paper, we let $f(x) = x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$ be an irreducible reciprocal polynomial, $\alpha $ a root of $f(x)$ and $L = F(\alpha )$ . Let $g(x)$ denote the minimal polynomial of $\alpha +1/\alpha $ . Thus, we have the following result as a consequence of Theorem 2.1.

Corollary 3.1. The polynomial $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$ is irreducible and defines a cubic subfield K of L.

Since $f(x)$ is irreducible of degree 6, it follows that $\operatorname {\mathrm {Gal}}(f)$ is a transitive subgroup of $S_6$ that is also a subgroup of $C_2 \wr S_3 \simeq S_4 \times C_2$ , by Corollary 2.2. Among the 16 transitive subgroups of $S_6$ , only 8 are subgroups of $S_4\times C_2$ . Table 1 gives information about these 8 groups: their transitive numbers (as given in [3]), their orders, descriptive names and generators for (one representative of the conjugacy class of) each group.

Table 1 Possible Galois groups of irreducible reciprocal sextic polynomials. Size gives the order of the group.

We point out that 6T7 and 6T8 are isomorphic copies of $S_4$ that are distinguished by their parity; that is, 6T7 contains only even permutations while 6T8 does not; this is reflected in the table by the respective superscripts of each group’s ‘Name’. Note that each of these eight groups does appear as a Galois group over $\mathbb {Q}$ . See Table 2, which gives one sample irreducible reciprocal sextic polynomial in $\mathbb {Q}[x]$ for each possible Galois group.

Table 2 One sample reciprocal sextic Polynomial in $\mathbb {Q}[x]$ for each possible Galois group.

We can determine properties of $\operatorname {\mathrm {Gal}}(f)$ from properties of $\operatorname {\mathrm {Gal}}(g)$ , as our next general result shows.

Theorem 3.2. Let $\phi (x)\in F[x]$ be irreducible of degree $6$ and $\rho $ be a root of $\phi $ . Suppose that $F(\rho )$ has a subfield M of degree $3$ defined by $\gamma (x)\in F[x]$ . Then:

1. (1) $\operatorname {\mathrm {Disc}}(\phi )$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(\phi )$ is either $A_4$ or $S_4^+$ ;

2. (2) $\operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(\phi )$ is either $C_6$ , $A_4$ or $A_4\times C_2$ ;

3. (3) $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(\phi )$ is either $S_3$ , $A_4$ or $S_4^-$ .

Proof. A standard result in Galois theory shows that $\operatorname {\mathrm {Gal}}(\phi )$ is a subgroup of $A_6$ if and only if $\operatorname {\mathrm {Disc}}(\phi )$ is a square in F. Of the eight possibilities, only $A_4$ and $S_4^+$ are subgroups of $A_6$ , proving item (1).

Since $\gamma $ is a cubic polynomial, another standard result in Galois theory shows $\operatorname {\mathrm {Gal}}(\gamma ) \simeq C_3$ if and only if $\operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square. Under the Galois correspondence, M corresponds to an index 3 subgroup H of $\operatorname {\mathrm {Gal}}(\phi )$ containing the stabiliser of $\rho $ . Let N be the normal core of H in $\operatorname {\mathrm {Gal}}(\phi )$ ; that is, the largest normal subgroup of $\operatorname {\mathrm {Gal}}(\phi )$ contained in H. Therefore, $\operatorname {\mathrm {Gal}}(\gamma )$ is isomorphic to $\operatorname {\mathrm {Gal}}(\phi )/N$ . Using [11] to perform group computations, we see that each of the eight possibilities has a unique such subgroup H of index 3, up to conjugation. This means $M/F$ is the unique cubic subfield of $F(\rho )/F$ , up to isomorphism. Further group computations show that in the cases of $C_6$ , $A_4$ and $A_4\times C_2$ , $\operatorname {\mathrm {Gal}}(\phi )/N$ is isomorphic to $C_3$ ; in all other cases it is isomorphic to $S_3$ , proving item (2).

If both $\operatorname {\mathrm {Disc}}(\phi )$ and $\operatorname {\mathrm {Disc}}(\gamma )$ are perfect squares, then $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square. According to the previous paragraphs, there is only one group among the eight where this occurs; namely, $A_4$ . For the remainder of the proof, we suppose neither $\operatorname {\mathrm {Disc}}(\phi )$ nor $\operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square. Thus, the polynomials $x^2-\operatorname {\mathrm {Disc}}(\phi )$ and $x^2-\operatorname {\mathrm {Disc}}(\gamma )$ define quadratic subfields of the splitting field of $\phi (x)$ . By the Galois correspondence, $F(\sqrt {\operatorname {\mathrm {Disc}}(\phi )})$ corresponds to $H_1=A_6\cap \operatorname {\mathrm {Gal}}(\phi )$ . Similarly, if $M'$ is the normal closure of $\gamma (x)$ , then the subgroup fixing $M'$ is N. Thus, $F(\sqrt {\operatorname {\mathrm {Disc}}(\gamma )})$ corresponds to the unique subgroup $H_2$ of $\operatorname {\mathrm {Gal}}(\phi )$ of index 2 that contains N. It follows that $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$ is a perfect square if and only if $H_1=H_2$ . Among the four remaining possible Galois groups, direct computation shows $S_3$ and $S_4^-$ have $H_1=H_2$ . The groups $D_6$ and $S_4\times C_2$ have $H_1\neq H_2$ , proving item (3).

Our next result is an immediate consequence of Theorem 3.2 and the fact that $\operatorname {\mathrm {Disc}}(f) = ((2a+c)^2-(2b+2)^2) \cdot \operatorname {\mathrm {Disc}}(g)^2$ .

Corollary 3.3. We have the following:

1. (1) $(2a+c)^2-(2b+2)^2$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(f)$ is either $A_4$ or $S_4^+$ ;

2. (2) $\operatorname {\mathrm {Disc}}(g)$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(f)$ is either $C_6$ , $A_4$ or $A_4\times C_2$ ;

3. (3) $((2a+c)^2-(2b+2)^2)\cdot \operatorname {\mathrm {Disc}}(g)$ is a perfect square in F if and only if $\operatorname {\mathrm {Gal}}(f)$ is either $S_3$ , $A_4$ or $S_4^-$ .

Next, we introduce a degree 4 resolvent polynomial that is helpful in determining $\operatorname {\mathrm {Gal}}(f)$ .

Theorem 3.4. Let $h(x) = x^4+Ax^3+Bx^2+Cx+D$ , where

• • $A = -4(a^2-2b-6)$ ;

• • $B = 2(3a^4 - 4a^2(3b+5) + 8(ac+b^2+4b+9))$ ;

• • $C = -4(a^4(a^2 - 6b-2) + 8a^2(ac+b^2 + 5) + 16(ac-2b^2 - b(ac+2) -4))$ ;

• • $D = (a^4-4a^2(b-1)+8(ac-2b))^2$ .

Then, $h(x)$ is separable and has a linear factor if and only if $\operatorname {\mathrm {Gal}}(f)$ is either $C_6$ , $S_3$ or $D_6$ .

Proof. Let $\{\alpha = r, 1/r, s, 1/s, t,1/t\}$ be the roots of $f(x)$ . The roots of $h(x)$ are $\{(r-1/r) \pm (s-1/s) \pm (t-1/t)\}$ , which can be verified by using the theory of elementary symmetric functions to express the coefficients of $h(x)$ in terms of a, b and c.

If $h(x)$ were not separable, then two roots would be equal. There are six cases:

1. (1) $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) + (s-1/s) - (t-1/t)$ ;

2. (2) $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$ ;

3. (3) $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$ ;

4. (4) $(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$ ;

5. (5) $(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$ ;

6. (6) $(r-1/r) - (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$ .

We will show each case leads to a contradiction. Cases 2 and 5 imply $s=1/s$ and Cases 1 and 6 imply $t=1/t$ ; these contradict the fact that $f(x)$ is irreducible and thus separable. Case 4 implies $st(s-t)=-(s-t)$ . Since $f(x)$ is separable, this implies $st=-1$ . Thus, $s=-1/t$ and $1/s=-t$ . Therefore, $-a = r+1/r+s+1/s+t+1/t = r+1/r$ , which is rational. However, this contradicts Theorem 2.1, which shows $r+1/r$ is not rational. Similarly, Case 3 implies $st(s+t)=s+t$ . If $s+t\neq 0$ , then $st=1$ ; which contradicts the separability of $f(x)$ . If $s=-t$ , then $1/s=-1/t$ . We again reach the contradiction $-a=r+1/r$ . Thus, $h(x)$ is separable.

To prove the rest of the theorem, let $G = S_4\times C_2$ and $H = D_6$ be the subgroups of $S_6$ as given in Table 1. Then, a complete set of a right coset representatives of $G/H$ is $\{\text {id}, (34), (56), (34)(56) \}$ . Further, the only block system of G is $R = \{\{1,2\}, \{3,4\}, \{5,6\}\}$ . We identify r as root 1, $1/r$ as root 2, s as root 3, $1/s$ as root 4, t as root 5 and $1/t$ as root 6.

A multivariable function stabilised by H is $T(x_1,x_2,x_3,x_4,x_5,x_6) = x_1-x_2+x_3-x_4+x_5-x_6$ ; the action on T is via subscripts. We form the resolvent polynomial corresponding to G, H and T (see [9]); this produces the polynomial $h(x)$ . By the theory of resolvent polynomials, the factorisation of $h(x)$ corresponds to the orbits of $\operatorname {\mathrm {Gal}}(f)$ acting on the cosets $G/H$ . Direct computation on each possibility for $\operatorname {\mathrm {Gal}}(f)$ shows that in the cases of $C_6$ , $S_3$ and $D_6$ , there is an orbit of length 1 and an orbit of length 3. In the other five cases, there is a single orbit of length 4. This means $h(x)$ factors as a linear times a cubic polynomial in those three cases and remains irreducible in the other five cases, proving the theorem.

We can now state our main result, which gives an elementary characterisation of $\operatorname {\mathrm {Gal}}(f)$ . This is an immediate consequence of Corollary 3.3 and Theorem 3.4. For convenience, Table 3 summarises this characterisation.

Table 3 Let $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$ be irreducible, $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$ and $h(x)$ as defined in Theorem 3.4. The table lists whether $\operatorname {\mathrm {Disc}}(f)$ , $\operatorname {\mathrm {Disc}}(g)$ and $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$ are perfect squares in F, and whether $h(x)$ has a linear factor, according to $\operatorname {\mathrm {Gal}}(f)$ .

Theorem 3.5. Let $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$ be irreducible, $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$ and $h(x)$ as defined in Theorem 3.4.

1. (1) If $\operatorname {\mathrm {Disc}}(f)$ is a perfect square in F, then $\operatorname {\mathrm {Gal}}(f)$ is $A_4$ if $\operatorname {\mathrm {Disc}}(g)$ is a square and is $S_4^+$ otherwise.

2. (2) If $\operatorname {\mathrm {Disc}}(f)$ is not a square and $\operatorname {\mathrm {Disc}}(g)$ is a square, then $\operatorname {\mathrm {Gal}}(f)$ is $C_6$ if $h(x)$ has a linear factor and is $A_4\times C_2$ otherwise.

3. (3) If $\operatorname {\mathrm {Disc}}(f)$ and $\operatorname {\mathrm {Disc}}(g)$ are not squares and $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$ is a square, then $\operatorname {\mathrm {Gal}}(f)$ is $S_3$ if $h(x)$ has a linear factor and is $S_4^-$ otherwise.

4. (4) If none of $\operatorname {\mathrm {Disc}}(f)$ , $\operatorname {\mathrm {Disc}}(g)$ and $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$ is a square, then $\operatorname {\mathrm {Gal}}(f)$ is $D_6$ if $h(x)$ has a linear factor and is $S_4\times C_2$ otherwise.

Example 3.6. As an example, we use Theorem 3.5 to compute the Galois group of a family of sextic reciprocal polynomials. Take $t>-27/4$ and suppose the polynomial $f(x) = x^6+3x^5+(t+6)x^4+(2t+7)x^3+(t+6)x^2+3x+1 \in \mathbb {Q}[x]$ is irreducible. Then, $\operatorname {\mathrm {Disc}}(f) = -t^4(4t+27)^3$ , which is not a square. We also have $g(x) = x^3 + 3x^2 + (t + 3)x + (2t + 1)$ . Then, $\operatorname {\mathrm {Disc}}(g) = -t^2(4t+27)$ , which is also not a square. However, $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$ is a square. Further, $h(x)$ has $x+4t+27$ as a linear factor. By item (3) of Theorem 3.5, $\operatorname {\mathrm {Gal}}(f)$ is $S_3$ . Note, this also confirms item (3) of [6, Theorem 1].

As an application of Theorem 3.5, we give one-parameter families of reciprocal sextics defined over $\mathbb {Q}$ for each possible Galois group.

Theorem 3.7. The polynomials in Table 4 have the indicated Galois group over $\mathbb {Q}$ , except for values of t that result in reducible polynomials.

Table 4 One-parameter families of reciprocal sextic polynomials with specified Galois group over $\mathbf {Q}$ .

Verifying each family of polynomials in Table 4 has the indicated Galois group is a straightforward computation using Theorem 3.5 and a computer algebra system. For example, we can consider the polynomial in the first row of Table 4: $f(x) = (2t^2{\kern-1pt}-2t+{\kern-1pt}13)x^6+(-4t+{\kern-1pt}2)x^5+(-2t^2{\kern-1pt}+{\kern-1pt}2t+19)x^4+(8t-4)x^3+(-2t^2+2t+19)x^2 +(-4t+2)x+(2t^2-2t+13)$ . Then, $\operatorname {\mathrm {Disc}}(f) = -(t^2-t-1)^4(t^2-t+7)^4$ , which is not a square. We also have $g(x) = (2t^2 - 2t + 13)x^3 + (-4t + 2)x^2 + (-8t^2 + 8t - 20)x + (16t - 8)$ . Then, $\operatorname {\mathrm {Disc}}(g) = (t^2-t-1)^2(t^2-t+7)^2$ , which is a square. Furthermore, $h(x)$ has $(t^4 - 2t^3 + 14t^2 - 13t + 169/4)x + 4t^4 - 8t^3 + 36t^2 - 32t + 64$ as a linear factor. This proves $\operatorname {\mathrm {Gal}}(f) = C_6$ , as claimed.