Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T02:31:45.288Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FIXED POINT PROPERTY IN DIRECT SUMS AND MODULUS 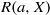$R(a, X)$

Part of: Normed linear spaces and Banach spaces; Banach lattices Nonlinear operators and their properties

Published online by Cambridge University Press:  28 June 2013

ANDRZEJ WIŚNICKI
ANDRZEJ WIŚNICKI*
Affiliation:
Institute of Mathematics, Maria Curie-Skłodowska University, 20-031 Lublin, Poland
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the direct sum 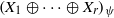$\mathop{({X}_{1} \oplus \cdots \oplus {X}_{r} )}\nolimits_{\psi } $ with a strictly monotone norm has the weak fixed point property for nonexpansive mappings whenever 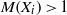$M({X}_{i} )\gt 1$ for each 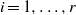$i= 1, \ldots , r$. In particular, 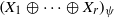$\mathop{({X}_{1} \oplus \cdots \oplus {X}_{r} )}\nolimits_{\psi } $ enjoys the fixed point property if Banach spaces 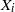${X}_{i} $ are uniformly nonsquare. This combined with the earlier results gives a definitive answer for 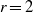$r= 2$: a direct sum 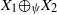${X}_{1} {\mathop{\oplus }\nolimits}_{\psi } {X}_{2} $ of uniformly nonsquare spaces with any monotone norm has the fixed point property. Our results are extended to asymptotically nonexpansive mappings in the intermediate sense.

Keywords

nonexpansive mappingasymptotically nonexpansive mappingfixed pointdirect sum

MSC classification

Secondary: 47H10: Fixed-point theorems 46B20: Geometry and structure of normed linear spaces 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 79 - 91
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ayerbe Toledano, J. M., Domínguez Benavides, T. and López Acedo, G., Measures of Noncompactness in Metric Fixed Point Theory (Birkhäuser, Basel, 1997).Google Scholar
Bauer, F. L., Stoer, J. and Witzgall, C., ‘Absolute and monotonic norms’, Numer. Math. 3 (1961), 257–264.CrossRefGoogle Scholar
Belluce, L. P., Kirk, W. A. and Steiner, E. F., ‘Normal structure in Banach spaces’, Pacific J. Math. 26 (1968), 433–440.CrossRefGoogle Scholar
Betiuk-Pilarska, A. and Prus, S., ‘Uniform nonsquareness of direct sums of Banach spaces’, Topol. Methods Nonlinear Anal. 34 (2009), 181–186.CrossRefGoogle Scholar
Betiuk-Pilarska, A. and Wiśnicki, A., ‘On the Suzuki nonexpansive-type mappings’, Ann. Funct. Anal. 4 (2) (2013), 72–86.CrossRefGoogle Scholar
Bonsall, F. F. and Duncan, J., Numerical Ranges. II (Cambridge University Press, Cambridge, 1973).Google Scholar
Dhompongsa, S., Kaewcharoen, A. and Kaewkhao, A., ‘Fixed point property of direct sums’, Nonlinear Anal. 63 (2005), e2177–e2188.Google Scholar
Dhompongsa, S. and Saejung, S., ‘Geometry of direct sums of Banach spaces’, Chamchuri J. Math. 2 (2010), 1–9.Google Scholar
Domínguez Benavides, T., ‘A geometrical coefficient implying the fixed point property and stability results’, Houston J. Math. 22 (1996), 835–849.Google Scholar
Domínguez Benavides, T., ‘A renorming of some nonseparable Banach spaces with the fixed point property’, J. Math. Anal. Appl. 350 (2009), 525–530.Google Scholar
García Falset, J., ‘Stability and fixed points for nonexpansive mappings’, Houston J. Math. 20 (1994), 495–506.Google Scholar
García Falset, J., Lloréns Fuster, E. and Mazcuñan Navarro, E. M., ‘Uniformly nonsquare Banach spaces have the fixed point property for nonexpansive mappings’, J. Funct. Anal. 233 (2006), 494–514.Google Scholar
Goebel, K., ‘On the structure of minimal invariant sets for nonexpansive mappings’, Ann. Univ. Mariae Curie-Skłodowska Sect. A 29 (1975), 73–77.Google Scholar
Goebel, K. and Kirk, W. A., Topics in Metric Fixed Point Theory (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Karlovitz, L. A., ‘Existence of fixed points of nonexpansive mappings in a space without normal structure’, Pacific J. Math. 66 (1976), 153–159.Google Scholar
Kato, M., Saito, K.-S. and Tamura, T., ‘Uniform non-squareness of $\psi $-direct sums of Banach spaces $X{\mathop{\oplus }\nolimits}_{\psi } Y$’, Math. Inequal. Appl. 7 (2004), 429–437.Google Scholar
Kato, M. and Tamura, T., ‘Weak nearly uniform smoothness and worth property of $\psi $-direct sums of Banach spaces’, Comment. Math. Prace Mat. 46 (2006), 113–129.Google Scholar
Kato, M. and Tamura, T., ‘Uniform non-${ \ell }_{1}^{n} $-ness of ${\ell }_{\infty } $-sums of Banach spaces’, Comment. Math. 49 (2009), 179–187.Google Scholar
Kirk, W. A., ‘A fixed point theorem for mappings which do not increase distances’, Amer. Math. Monthly 72 (1965), 1004–1006.CrossRefGoogle Scholar
Kirk, W. A. and Martinez-Yanez, C., ‘Nonexpansive and locally nonexpansive mappings in product spaces’, Nonlinear Anal. 12 (1988), 719–725.Google Scholar
Kirk, W. A. and Sims, B. (eds.) Handbook of Metric Fixed Point Theory (Kluwer Academic Publishers, Dordrecht, 2001).Google Scholar
Kuczumow, T., ‘Fixed point theorems in product spaces’, Proc. Amer. Math. Soc. 108 (1990), 727–729.Google Scholar
Prus, S., ‘Banach spaces which are uniformly noncreasy’, in: Proc. 2nd World Congress of Nonlinear Analysts, Nonlinear Anal., 30 (ed. Lakshmikantham, V.) (1997), 2317–2324.Google Scholar
Saito, K.-S., Kato, M. and Takahashi, Y., ‘Von Neumann-Jordan constant of absolute normalized norms on ${ \mathbb{C} }^{2} $’, J. Math. Anal. Appl. 244 (2000), 515–532.Google Scholar
Saito, K.-S., Kato, M. and Takahashi, Y., ‘Absolute norms on ${ \mathbb{C} }^{n} $’, J. Math. Anal. Appl. 252 (2000), 879–905.Google Scholar
Sims, B. and Smyth, M. A., ‘On some Banach space properties sufficient for weak normal structure and their permanence properties’, Trans. Amer. Math. Soc. 351 (1999), 497–513.Google Scholar
Takahashi, Y., Kato, M. and Saito, K.-S., ‘Strict convexity of absolute norms on ${ \mathbb{C} }^{2} $ and direct sums of Banach spaces’, J. Inequal. Appl. 7 (2002), 179–186.Google Scholar
Wiśnicki, A., ‘Products of uniformly noncreasy spaces’, Proc. Amer. Math. Soc. 130 (2002), 3295–3299.Google Scholar
Wiśnicki, A., ‘On the fixed points of nonexpansive mappings in direct sums of Banach spaces’, Studia Math. 207 (2011), 75–84.Google Scholar
Wiśnicki, A., ‘The super fixed point property for asymptotically nonexpansive mappings’, Fund. Math. 217 (2012), 265–277.Google Scholar