Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T16:56:43.196Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITELY STABLE ADDITIVE BASES

Part of: Additive number theory; partitions Sequences and sets

Published online by Cambridge University Press:  20 February 2018

L. A. FERREIRA Open the ORCID record for L. A. FERREIRA [Opens in a new window]
L. A. FERREIRA*
Affiliation:
Institute of Mathematics and Statistics of University of São Paulo, Rua do Matão, 1010, Cidade Universitária, São Paulo, SP 05508-090, Brazil email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An additive basis 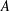$A$ is finitely stable when the order of 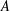$A$ is equal to the order of 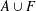$A\cup F$ for all finite subsets 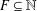$F\subseteq \mathbb{N}$. We give a sufficient condition for an additive basis to be finitely stable. In particular, we prove that 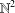$\mathbb{N}^{2}$ is finitely stable.

Keywords

additive basesadditive number theorysum of squares

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11P05: Waring's problem and variants
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 360 - 362
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Landau, E., ‘Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindestzahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate’, Arch. Math. Phys. 13(3) (1908), 305–312.Google Scholar
Nathanson, M. B., Additive Number Theory: The Classical Bases, Graduate Texts in Mathematics, 164 (Springer, New York, 1996).CrossRefGoogle Scholar