Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T06:07:12.802Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE UNITARY RINGS IN WHICH ALL SYLOW SUBGROUPS OF THE GROUP OF UNITS ARE CYCLIC

Part of: Chain conditions, growth conditions, and other forms of finiteness Conditions on elements

Published online by Cambridge University Press:  13 February 2019

M. AMIRI Open the ORCID record for M. AMIRI [Opens in a new window]  and
M. ARIANNEJAD Open the ORCID record for M. ARIANNEJAD [Opens in a new window]
M. AMIRI
Affiliation:
Departamento de Matemática-ICE-UFAM, 69080-900, Manaus-AM, Brazil email [email protected]
M. ARIANNEJAD*
Affiliation:
Department of Mathematics, University of Zanjan, Zanjan, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterise finite unitary rings 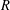$R$ such that all Sylow subgroups of the group of units 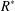$R^{\ast }$ are cyclic. To be precise, we show that, up to isomorphism, 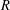$R$ is one of the three types of rings in 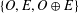$\{O,E,O\oplus E\}$, where 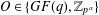$O\in \{GF(q),\mathbb{Z}_{p^{\unicode[STIX]{x1D6FC}}}\}$ is a ring of odd cardinality and 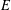$E$ is a ring of cardinality 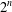$2^{n}$ which is one of seven explicitly described types.

Keywords

finite ringgroup of unitsSylow subgroup

MSC classification

Primary: 16U60: Units, groups of units
Secondary: 16P10: Finite rings and finite-dimensional algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 403 - 412
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This work has been partially supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) of the Ministry of Education of Brazil.

References

Dolzan, D., ‘Nilpotency of the group of units of a finite ring’, Bull. Aust. Math. Soc. 79 (2009), 177–182.Google Scholar
Eldridge, K. E., ‘Orders for finite noncommutative rings with unity’, Amer. Math. Monthly 75 (1968), 512–514.Google Scholar
Erickson, D. B., ‘Orders for finite noncommutative rings’, Amer. Math. Monthly 73 (1966), 376–377.Google Scholar
Farb, B. and Keith Dennis, R., Noncommutative Algebra, Graduate Texts in Mathematics, 144 (Springer, New York, 1993).Google Scholar
Groza, G., ‘Artinian rings having a nilpotent group of units’, J. Algebra 121 (1989), 253–262.Google Scholar
Lam, T. Y., A First Course in Noncommutative Rings, Graduate Texts in Mathematics, 2nd edn (Springer, New York, 2001).Google Scholar
Wedderburn, J. H. M., ‘A theorem on finite algebra’, Trans. Amer. Math. Soc. 6 (1905), 349–352; 1996.Google Scholar