Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T20:40:25.620Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE HIGHER COMMUTATORS IN ASSOCIATIVE RINGS

Part of: Rings with polynomial identity Modules, bimodules and ideals Rings and algebras with additional structure

Published online by Cambridge University Press:  27 September 2013

CHARLES LANSKI
CHARLES LANSKI*
Affiliation:
Department of Mathematics, University of Southern California, 3620 South Vermont Avenue, Los Angeles, CA 90089-2532, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 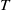$T$ is any finite higher commutator in an associative ring 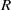$R$, for example, 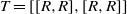$T= [[R, R] , [R, R] ] $, and if 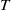$T$ has minimal cardinality so that the ideal generated by 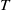$T$ is infinite, then 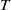$T$ is in the centre of 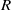$R$ and 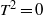${T}^{2} = 0$. Also, if 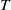$T$ is any finite, higher commutator containing no nonzero nilpotent element then 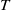$T$ generates a finite ideal.

Keywords

higher commutatorscommutator identitiesfinite ideals

MSC classification

Secondary: 16W10: Rings with involution; Lie, Jordan and other nonassociative structures 16R50: Other kinds of identities (generalized polynomial, rational, involution) 16D25: Ideals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 503 - 509
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bell, H. E., ‘Higher derivatives and finiteness in rings’, Math. J. Okayama Univ. 41 (1999), 21–25.Google Scholar
Bell, H. E. and Klein, A., ‘Combinatorial commutativity and finiteness conditions for rings’, Comm. Algebra 29 (2001), 2935–2943.Google Scholar
Herstein, I. N., Noncommutative Rings, Carus Monograph, 15 (Mathematical Association of America, Buffalo, NY, 1968).Google Scholar
Hirano, Y., ‘Some finiteness conditions for rings’, Chinese J. Math. 16 (1988), 55–59.Google Scholar
Hirano, Y., ‘On a problem of Szász’, Bull. Aust. Math. Soc. 40 (1989), 363–364.Google Scholar
Kaplansky, I., Fields and Rings, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, 1969).Google Scholar
Koh, K., ‘On properties of rings with a finite number of zero divisors’, Math. Ann. 171 (1976), 79–80.Google Scholar
Lanski, C., ‘Higher commutators, ideals, and cardinality’, Bull. Aust. Math. Soc. 54 (1996), 41–54.Google Scholar
Lanski, C., ‘Rings with few nilpotents’, Houston J. Math. 18 (1992), 577–590.Google Scholar
Lanski, C., ‘On the cardinality of rings with special subsets which are finite’, Houston J. Math. 19 (1993), 357–373.Google Scholar
Lanski, C., Concepts in Abstract Algebra, Brooks/Cole Series in Advanced Mathematics (Thomson Brooks/Cole, Belmont, CA, 2005).Google Scholar