Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T03:56:49.170Z Has data issue: false hasContentIssue false
  • English
  • Français

FINDING INVOLUTIONS WITH SMALL SUPPORT

Part of: Probabilistic methods in group theory Representation theory of groups Permutation groups

Published online by Cambridge University Press:  11 January 2016

ALICE C. NIEMEYER  and
TOMASZ POPIEL
ALICE C. NIEMEYER*
Affiliation:
Lehrstuhl B für Mathematik, RWTH Aachen University, Pontdriesch 10–16, 52062 Aachen, Germany email [email protected]
TOMASZ POPIEL
Affiliation:
Centre for the Mathematics of Symmetry and Computation, School of Mathematics and Statistics, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the proportion of permutations 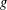$g$ in 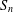$S_{\!n}$ or 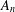$A_{n}$ such that 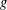$g$ has even order and 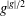$g^{|g|/2}$ is an involution with support of cardinality at most 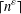$\lceil n^{{\it\varepsilon}}\rceil$ is at least a constant multiple of ${\it\varepsilon}$. Using this result, we obtain the same conclusion for elements in a classical group of natural dimension $n$ in odd characteristic that have even order and power up to an involution with 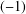$(-1)$-eigenspace of dimension at most 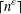$\lceil n^{{\it\varepsilon}}\rceil$ for a linear or unitary group, or 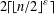$2\lceil \lfloor n/2\rfloor ^{{\it\varepsilon}}\rceil$ for a symplectic or orthogonal group.

Keywords

symmetric groupalternating groupclassical groupproportion of elementsinvolution

MSC classification

Primary: 20D06: Simple groups
Secondary: 20P05: Probabilistic methods in group theory 20B30: Symmetric groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 43 - 47
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Beals, R., Leedham-Green, C. R., Niemeyer, A. C., Praeger, C. E. and Seress, Á., ‘Permutations with restricted cycle structure and an algorithmic application’, Combin. Probab. Comput. 11 (2002), 447–464.Google Scholar
Beals, R., Leedham-Green, C. R., Niemeyer, A. C., Praeger, C. E. and Seress, Á., ‘A black-box group algorithm for recognizing finite symmetric and alternating groups. I’, Trans. Amer. Math. Soc. 355 (2003), 2097–2113.Google Scholar
Beals, R., Leedham-Green, C. R., Niemeyer, A. C., Praeger, C. E. and Seress, Á., ‘Constructive recognition of finite alternating and symmetric groups acting as matrix groups on their natural permutation modules’, J. Algebra 292 (2005), 4–46.Google Scholar
Bratus, S. and Pak, I., ‘Fast constructive recognition of a black box group isomorphic to S n or A n using Goldbach’s conjecture’, J. Symbolic Comput. 29 (2000), 33–57.Google Scholar
Bray, J. N., ‘An improved method for generating the centralizer of an involution’, Arch. Math. (Basel) 74 (2000), 241–245.Google Scholar
Jambor, S., Leuner, M., Niemeyer, A. C. and Plesken, W., ‘Fast recognition of alternating groups of unknown degree’, J. Algebra 392 (2013), 315–335.Google Scholar
Lübeck, F., Niemeyer, A. C. and Praeger, C. E., ‘Finding involutions in finite Lie type groups of odd characteristic’, J. Algebra 321 (2009), 3397–3417.Google Scholar
Niemeyer, A. C., Popiel, T., Praeger, C. E. and Yalçınkaya, Ş., ‘On semiregular permutations of a finite set’, Math. Comp. 81 (2012), 605–622.Google Scholar
O’Brien, E. A., ‘Algorithms for matrix groups’, in: Groups St. Andrews 2009 in Bath, II, London Mathematical Society Lecture Note Series, 388 (Cambridge University Press, Cambridge, 2011), 297–323.Google Scholar