Article contents
Exponential actions, orbits and their kernels
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 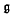 be a nilpotent Lie algebra which is an exponential
be a nilpotent Lie algebra which is an exponential 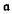 -module,
-module, 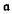 being an exponential algebra of derivations of
being an exponential algebra of derivations of 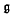 . Put
. Put 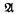 = exp
= exp 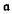 and
and 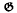 = exp
= exp 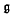 . If Ω is a closed orbit of
. If Ω is a closed orbit of 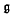 * under the action of
* under the action of 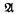 , then Ker
, then Ker 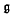 is dense in Ker Ω for the topology of L1 (
is dense in Ker Ω for the topology of L1 (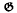 ) and the algebra Ker
) and the algebra Ker 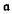 is nilpotent, where
is nilpotent, where 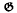 denotes the minimal closed ideal of L1(
denotes the minimal closed ideal of L1(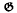 ) whose hull is Ω. Moreover, the
) whose hull is Ω. Moreover, the 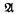 -prime ideals of Ll(
-prime ideals of Ll(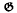 ) coincide with the kernels Ker Ω, where Ω denotes an arbitrary orbit (not necessarily closed) in
) coincide with the kernels Ker Ω, where Ω denotes an arbitrary orbit (not necessarily closed) in 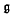 *.
*.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1998
References
[1]Bernat, P., Conze, N., Duflo, M., Lévy-Nahas, M., Rais, M., Renouard, P. and Vergne, M., Représentations des groupes de Lie résolubles (Dunod, Paris, 1972).Google Scholar
[2]Boidol, J., Leptin, H., Schürman, J. and Vahle, D., ‘Räume primitiver Ideale von Gruppen-algebren’, Math. Ann. 236 (1978), 1–13.CrossRefGoogle Scholar
[3]Brown, I., ‘Dual topology of a nilpotent Lie group’, Ann. Sci. École Norm. Sup. 6 (1973), 407–411.CrossRefGoogle Scholar
[4]Dixmier, J., ‘Opérateurs de rang fini dans les représentations unitaires’, Inst. Hautes Études Sci. Publ. Math. 6 (1960), 305–317.CrossRefGoogle Scholar
[5]Dixmier, J., Les C*-algèbres et leurs représentations (Gauthier-Villars, Paris, 1969).Google Scholar
[6]Hochschild, G., The structure of Lie groups (Holden-Day Inc., San Francisco, London, Amsterdam, 1965).Google Scholar
[7]Howe, R., ‘On a connection between nilpotent groups and oscillatory integrals associated to singularities‘, Pacific J. Math. 73 (1977), 329–363.CrossRefGoogle Scholar
[8]Hulanicki, A., ‘A functional calculus for Rockland operators on nilpotent Lie groups’, Stud. Math. 78 (1984), 253–266.CrossRefGoogle Scholar
[9]Kirillov, A.A., ‘Unitary representations of nilpotent Lie groups’, Uspekhi Mat. Nauk. 17 (1962), 53–104.Google Scholar
[10]Leptin, H., ‘Ideal theory in group algebras of locally compact groups’, Invent. Math. 31 (1976), 259–278.CrossRefGoogle Scholar
[11]Leptin, H. and Ludwig, J., Unitary representation theory of exponential Lie groups, De Gruyter Expositions in Mathematics 18 (De Gruyter, Berlin, New York, 1994).CrossRefGoogle Scholar
[12]Ludwig, J., ‘On the spectral synthesis problem for points in the dual of a nilpotent Lie group’, Ark. Mat. 21 (1983), 127–144.CrossRefGoogle Scholar
[13]Ludwig, J., ‘Irreducible representations of exponential solvable Lie groups and operators with smooth kernels’, J. Reine Angew. Math. 339 (1983), 1–26.Google Scholar
[14]Ludwig, J., ‘On primary ideals in the group algebra of a nilpotent Lie group’, Math. Ann. 262 (1983), 287–304.CrossRefGoogle Scholar
[15]Ludwig, J., ‘Minimal C*-dense ideals and algebraically irreducible representations of the Schwartz-algebra of a nilpotent Lie group’, in Harmonic analysis, Lecture Notes in Math. 1359 (Springer Verlag, Berlin, Heidelberg, New York, 1987), pp. 209–217.CrossRefGoogle Scholar
[16]Ludwig, J. and Molitor-Braun, C., ‘Algèbre de Schwartz d'un groupe de Lie nilpotent’, Centre Univ. Luxembourg, Travaux mathématiques VII (1995), 25–67.Google Scholar
[17]Ludwig, J., Rosenbaum, G. and Samuel, J., ‘The elements of bounded trace in the C*-algebra of a nilpotent Lie group’, Invent. Math. 83 (1986), 167–190.CrossRefGoogle Scholar
[19]Molitor-Braun, C., ‘Actions exponentielles et noyaux d'opérateurs’, Centre Univ. Luxembourg, Travaux mathématigues IX (1997), 23–101.Google Scholar
[20]Poguntked, D., ‘Algebraically irreducible representations of L1-algebras of exponential Lie groups’, Duke Math. J. 50 (1983), 1077–1106.Google Scholar
[21]Poguntke, D., ‘Über das Synthese-problem für nilpotente Liesche Gruppen’, Math. Ann. 269 (1984), 431–467.CrossRefGoogle Scholar
[22]Pukanszky, L., ‘On the unitary representations of exponential groups’, J. Funct. Anal. 2 (1968), 73–113.CrossRefGoogle Scholar
- 6
- Cited by


