Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fisher, Evan
Berman, Matthew
Vowels, Natalie
and
Wilson, Christine
2000.
Excursions of a normal random walk above a boundary.
Statistics & Probability Letters,
Vol. 48,
Issue. 2,
p.
141.
Buldygin, Valeriĭ V.
Indlekofer, Karl-Heinz
Klesov, Oleg I.
and
Steinebach, Josef G.
2018.
Pseudo-Regularly Varying Functions and Generalized Renewal Processes.
Vol. 91,
Issue. ,
p.
419.


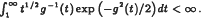 .
.