Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-29T01:01:25.065Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF TRAVELLING WAVES IN THE FRACTIONAL BURGERS EQUATION

Part of: Representations of solutions Miscellaneous topics - Partial differential equations Singular integral equations Partial differential equations

Published online by Cambridge University Press:  20 December 2017

ADAM CHMAJ Open the ORCID record for ADAM CHMAJ [Opens in a new window]
ADAM CHMAJ*
Affiliation:
Freelance, Warsaw, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct travelling waves in the Burgers equation with the fractional Laplacian 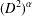$(D^{2})^{\unicode[STIX]{x1D6FC}}$, 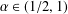$\unicode[STIX]{x1D6FC}\in (1/2,1)$. This is done by first constructing odd solutions 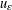$u_{\unicode[STIX]{x1D700}}$ of 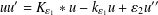$uu^{\prime }=K_{\unicode[STIX]{x1D700}_{1}}\ast u-k_{\unicode[STIX]{x1D700}_{1}}u+\unicode[STIX]{x1D700}_{2}u^{\prime \prime }$, 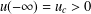$u(-\infty )=u_{c}>0$, with 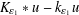$K_{\unicode[STIX]{x1D700}_{1}}\ast u-k_{\unicode[STIX]{x1D700}_{1}}u$ nonsingular, and then passing to the limit 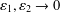$\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2}\rightarrow 0$, to give 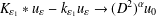$K_{\unicode[STIX]{x1D700}_{1}}\ast u_{\unicode[STIX]{x1D700}}-k_{\unicode[STIX]{x1D700}_{1}}u_{\unicode[STIX]{x1D700}}\rightarrow (D^{2})^{\unicode[STIX]{x1D6FC}}u_{0}$ pointwise. The proof relies on operator splitting.

Keywords

singular integral equationtravelling waves

MSC classification

Primary: 45E10: Integral equations of the convolution type (Abel, Picard, Toeplitz and Wiener-Hopf type)
Secondary: 35A01: Existence problems 35C07: Traveling wave solutions 35R11: Fractional partial differential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 102 - 109
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Alibaud, N., ‘Entropy formulation for fractal conservation laws’, J. Evol. Equ. 7 (2007), 145–175.CrossRefGoogle Scholar
Alibaud, N. and Andreianov, B., ‘Non-uniqueness of weak solutions for the fractal Burgers equation’, Ann. Inst. H. Poincaré Anal. Non Linéaire 27 (2010), 997–1016.Google Scholar
Alibaud, N., Droniou, J. and Vovelle, J., ‘Occurrence and non-appearance of shocks in fractal Burgers equations’, J. Hyperbolic Differ. Equ. 4 (2007), 479–499.Google Scholar
Alibaud, N., Imbert, C. and Karch, G., ‘Asymptotic properties of entropy solutions to fractal Burgers equation’, SIAM J. Math. Anal. 42 (2010), 354–376.Google Scholar
Biler, P., Funaki, T. and Woyczynski, W., ‘Fractal Burgers equations’, J. Differ. Equ. 148 (1998), 9–46.Google Scholar
Chan, C. H., Czubak, M. and Silvestre, L., ‘Eventual regularization of the slightly supercritical fractional Burgers equation’, Discrete Contin. Dyn. Syst. 27 (2010), 847–861.Google Scholar
Chen, X. and Jiang, H., ‘Traveling waves of a non-local conservation law’, Differ. Integral Equ. 25 (2012), 1143–1174.Google Scholar
Chmaj, A., ‘Existence of traveling waves for the nonlocal Burgers equation’, Appl. Math. Lett. 20 (2007), 439–444.CrossRefGoogle Scholar
Chmaj, A., ‘Existence of traveling waves in the fractional bistable equation’, Arch. Math. (Basel) 100 (2013), 473–480.CrossRefGoogle Scholar
Droniou, J., Gallouet, T. and Vovelle, J., ‘Global solution and smoothing effect for a non-local regularization of a hyperbolic equation’, J. Evol. Equ. 3 (2003), 499–521.Google Scholar
Karch, G., Miao, C. and Xu, X., ‘On convergence of solutions of fractal Burgers equation toward rarefaction waves’, SIAM J. Math. Anal. 39 (2008), 1536–1549.Google Scholar
Kiselev, A., Nazarov, F. and Shterenberg, R., ‘Blow up and regularity for fractal Burgers equation’, Dyn. Partial Differ. Equ. 5 (2008), 211–240.CrossRefGoogle Scholar
Silvestre, L., ‘On the differentiability of the solution to the Hamilton–Jacobi equation with critical fractional diffusion’, Adv. Math. 226 (2011), 2020–2039.Google Scholar