Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mustafa, Octavian G.
and
Tunç, Cemil
2009.
Asymptotically linear solutions of differential equations via Lyapunov functions.
Applied Mathematics and Computation,
Vol. 215,
Issue. 8,
p.
3076.
Băleanu, Dumitru
and
Mustafa, Octavian G.
2009.
On the asymptotic integration of a class of sublinear fractional differential equations.
Journal of Mathematical Physics,
Vol. 50,
Issue. 12,
Jarad, Fahd
Mustafa, Octavian G.
and
O'Regan, Donal
2012.
Positive solutions of some elliptic differential equations with oscillating nonlinearity.
Complex Variables and Elliptic Equations,
Vol. 57,
Issue. 6,
p.
599.
Mustafa, Octavian G.
2012.
Oscillatory solutions of some integrable differential equations.
Monatshefte für Mathematik,
Vol. 165,
Issue. 2,
p.
251.
Jin, Liangbing
and
Li, Chunming
2013.
Positive solutions to a class of second-order semilinear elliptic equations in an exterior domain.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 79,
Issue. ,
p.
233.


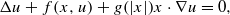
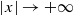 under quite general assumptions upon
under quite general assumptions upon 