Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-07T11:02:05.666Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATES OF THE SECOND DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS

Part of: Geometric function theory Riemann surfaces

Published online by Cambridge University Press:  03 June 2019

GANGQIANG CHEN Open the ORCID record for GANGQIANG CHEN [Opens in a new window]
GANGQIANG CHEN*
Affiliation:
Graduate School of Information Sciences, Tohoku University, Aoba-ku, Sendai 980-8579, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume a point $z$ lies in the open unit disk 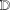$\mathbb{D}$ of the complex plane 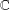$\mathbb{C}$ and 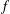$f$ is an analytic self-map of 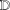$\mathbb{D}$ fixing 0. Then Schwarz’s lemma gives 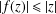$|f(z)|\leq |z|$, and Dieudonné’s lemma asserts that 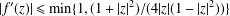$|f^{\prime }(z)|\leq \min \{1,(1+|z|^{2})/(4|z|(1-|z|^{2}))\}$. We prove a sharp upper bound for 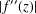$|f^{\prime \prime }(z)|$ depending only on 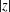$|z|$.

Keywords

bounded analytic functionsSchwarz’s lemmaDieudonné’s lemma

MSC classification

Primary: 30C80: Maximum principle; Schwarz's lemma, Lindelöf principle, analogues and generalizations; subordination
Secondary: 30F45: Conformal metrics (hyperbolic, Poincaré, distance functions)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 458 - 469
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Avkhadiev, F. G. and Wirths, K.-J., Schwarz–Pick Type Inequalities (Birkhäuser, Basel, 2009).Google Scholar
Cho, K. H., Kim, S.-A. and Sugawa, T., ‘On a multi-point Schwarz–Pick lemma’, Comput. Methods Funct. Theory 12(2) (2012), 483–499.10.1007/BF03321839Google Scholar
Dieudonné, J., ‘Recherches sur quelques problèmes relatifs aux polynômes et aux fonctions bornées d’une variable complexe’, Ann. Sci. Éc. Norm. Supér. 48 (1931), 247–358.10.24033/asens.812Google Scholar
Kaptanoğlu, H. T., ‘Some refined Schwarz–Pick lemmas’, Michigan Math. J. 50(3) (2002), 649–664.Google Scholar
Kim, S.-A. and Sugawa, T., ‘Invariant differential operators associated with a conformal metric’, Michigan Math. J. 55(2) (2007), 459–479.Google Scholar
Peschl, E., ‘Les invariants différentiels non holomorphes et leur rôle dans la théorie des fonctions’, Rend. Sem. Mat. Messina 1 (1955), 100–108.Google Scholar
Rivard, P., ‘Some applications of higher-order hyperbolic derivatives’, Complex Anal. Oper. Theory 7(4) (2013), 1127–1156.Google Scholar
Rogosinski, W., ‘Zum Schwarzschen Lemma’, Jahresber. Dtsch. Math.-Ver. 44 (1934), 258–261.Google Scholar
Ruscheweyh, St., ‘Two remarks on bounded analytic functions’, Serdica 11(2) (1985), 200–202.Google Scholar
Szász, O., ‘Ungleichheitsbeziehungen für die Ableitungen einer Potenzreihe, die eine im Einheitskreise beschränkte Funktion darstellt’, Math. Z. 8(3–4) (1920), 303–309.Google Scholar
Yamashita, S., ‘The Pick version of the Schwarz lemma and comparison of the Poincaré densities’, Ann. Acad. Sci. Fenn. Math. 19(2) (1994), 291–322.Google Scholar