Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T04:02:28.262Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ERROR TERM IN THE SATO–TATE THEOREM OF BIRCH

Part of: Arithmetic algebraic geometry Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  08 February 2019

M. RAM MURTY  and
NEHA PRABHU Open the ORCID record for NEHA PRABHU [Opens in a new window]
M. RAM MURTY
Affiliation:
Queen’s University, Kingston, Ontario K7L 3N6, Canada email [email protected]
NEHA PRABHU*
Affiliation:
Queen’s University, Kingston, Ontario K7L 3N6, Canada email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish an error term in the Sato–Tate theorem of Birch. That is, for 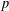$p$ prime, 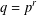$q=p^{r}$ and an elliptic curve $E:y^{2}=x^{3}+ax+b$, we show that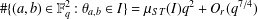

$$\begin{eqnarray}\#\{(a,b)\in \mathbb{F}_{q}^{2}:\unicode[STIX]{x1D703}_{a,b}\in I\}=\unicode[STIX]{x1D707}_{ST}(I)q^{2}+O_{r}(q^{7/4})\end{eqnarray}$$
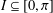for any interval $I\subseteq [0,\unicode[STIX]{x1D70B}]$, where the quantity $\unicode[STIX]{x1D703}_{a,b}$ is defined by 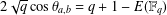$2\sqrt{q}\cos \unicode[STIX]{x1D703}_{a,b}=q+1-E(\mathbb{F}_{q})$ and 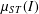$\unicode[STIX]{x1D707}_{ST}(I)$ denotes the Sato–Tate measure of the interval 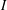$I$.

Keywords

Sato–Tate theoremelliptic curves

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11K38: Irregularities of distribution, discrepancy
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 27 - 33
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Baier, S. and Zhao, L., ‘The Sato–Tate conjecture on average for small angles’, Trans. Amer. Math. Soc. 361(4) (2009), 1811–1832.Google Scholar
Banks, W. D. and Shparlinski, I. E., ‘Sato–Tate, cyclicity, and divisibility statistics on average for elliptic curves of small height’, Israel J. Math. 173 (2009), 253–277.Google Scholar
Birch, B. J., ‘How the number of points of an elliptic curve over a fixed prime field varies’, J. Lond. Math. Soc. 43 (1968), 57–60.Google Scholar
David, C., Koukoulopoulos, D. and Smith, E., ‘Sums of Euler products and statistics on elliptic curves’, Math. Ann. 368 (2017), 685–752.Google Scholar
Deligne, P., ‘Formes modulaires et représentations l-adiques’, in: Séminaire Bourbaki, Vol. 1968/69, Exp. No. 355, Lecture Notes in Mathematics, 175 (Springer, Berlin, 1971), 139–172.Google Scholar
Deligne, P., ‘La conjecture de Weil. I’, Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.Google Scholar
Deligne, P., ‘La conjecture de Weil. II’, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.Google Scholar
Deuring, M., ‘Die Typen der Multiplikatorenringe elliptischer Funktionenkörper’, Abh. Math. Semin. Univ. Hambg. 14 (1941), 197–272.Google Scholar
Fisher, B., ‘Equidistribution theorems’, in: Columbia University Number Theory Seminar, New York, 1992, Astérisque, 228 (Société Mathématique de France, Paris, 1995), 69–79.Google Scholar
Katz, N. M., Gauss Sums, Kloosterman Sums, and Monodromy Groups (Princeton University Press, Princeton, NJ, 1988).Google Scholar
Knightly, A. and Li, C., Traces of Hecke Operators, Mathematical Surveys and Monographs, 133 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Lang, S., Introduction to Modular Forms, Fundamental Principles of Mathematical Sciences, 222 (Springer, Berlin, 1995), with appendixes by D. Zagier and Walter Feit, corrected reprint of the 1976 original.Google Scholar
Lenstra, H. W. Jr, ‘Factoring integers with elliptic curves’, Ann. of Math. (2) 126(3) (1987), 649–673.Google Scholar
Michel, P., ‘Rang moyen de familles de courbes elliptiques et lois de Sato–Tate’, Monatsh. Math. 120 (1995), 127–136.Google Scholar
Miller, S. J. and Ram Murty, M., ‘Effective equidistribution and the Sato–Tate law for families of elliptic curves’, J. Number Theory 131 (2011), 25–44.Google Scholar
Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis, CBMS Regional Conference Series in Mathematics, 84 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Ram Murty, M., ‘Oscillations of Fourier coefficients of modular forms’, Math. Ann. 262 (1983), 431–446.Google Scholar
Ram Murty, M. and Sinha, K., ‘Effective equidistribution of eigenvalues of Hecke operators’, J. Number Theory 129 (2009), 681–714.Google Scholar
Niederreiter, H., ‘The distribution of values of Kloosterman sums’, Arch. Math. 56 (1991), 270–277.Google Scholar
Schoof, R., ‘Nonsingular plane cubic curves over finite fields’, J. Combin. Theory Ser. A 46(2) (1987), 183–211.Google Scholar