Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-11T18:38:12.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariance and imprimivity for discrete Hopf C*-coactions

Published online by Cambridge University Press:  17 April 2009

S. Kaliszewski  and
John Quigg
S. Kaliszewski
Affiliation:
Department of Mathematics, Arizona State University, Tempe AZ 85287, United States of America, e-mail: [email protected], [email protected]
John Quigg
Affiliation:
Department of Mathematics, Arizona State University, Tempe AZ 85287, United States of America, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let U, V, and W be multiplicative unitaries coming from discrete Kac systems such that W is an amenable normal submultiplicative unitary of V with quotient U. We define notions for right-Hilbert bimodules of coactions of SV and ŜV, their restrictions to SW and ŜU, their dual coactions, and their full and reduced crossed products. If N (A) denotes the imprimitivity bimodule associated to a coaction δ of SV on a C*-algebra A by Ng's imprimitivity theorem, we prove that for a suitably nondegenerate injective right-Hilbert bimodule coaction of SV on AXB, the balanced tensor products 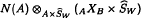and 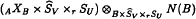are isomorphic right-Hilbert A×ŜV×rSU − B × ŜW bimodules. This can be interpreted as a natural equivalence between certain crossed-product functors.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 62 , Issue 2 , October 2000 , pp. 253 - 272
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Baaj, S. and Skandalis, G., ‘C*-algèbres de Hopf et théorie de Kasparov équivariante’, K-Theory 2 (1989), 683–721.CrossRefGoogle Scholar
[2]Baaj, S. and Skandalis, G., ‘Unitaires multiplicatifs et dualité pour les produits croisés de C*-algebres’, Ann. Sci. École Norm. Sup. 26 (1993), 425–488.CrossRefGoogle Scholar
[3]Echterhoff, S., ‘Duality of induction and restriction for abelian twisted covariant systems’, Math. Proc. Camb. Philos. Soc. 116 (1994), 301–315.CrossRefGoogle Scholar
[4]Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Imprimitivity theorems as natural equivalences’, (in preparation, 2000).Google Scholar
[5]Echterhoff, S., Kaliszewski, S. and Raeburn, I., ‘Crossed products by dual coactions of groups and homogeneous spaces’, J. Operator Theroy 39 (1998), 151–176.Google Scholar
[6]Echterhoff, S. and Raeburn, I., ‘Multipliers of imprimitivity bimodules and Morita equivalence of crossed products’, Math. Scand. 76 (1995), 289–309.CrossRefGoogle Scholar
[7]Echterhoff, S. and Raeburn, I., ‘The stabilisation trick for coactions’, J. reine angew. Math. 470 (1996), 181–215.Google Scholar
[8]Gootman, E. and Lazar, A., ‘Applications of non-commutative duality to crossed product C*-algebras determined by an action or coaction’, Proc. London Math. Soc. 59 (1989), 593–624.CrossRefGoogle Scholar
[9]Green, P., ‘The local structure of twisted covariance algebras’, Acta Math. 140 (1978), 191–250.CrossRefGoogle Scholar
[10]Imai, S. and Takai, H., ‘On a duality for C*-crossed products by a locally compact group’, J. Math. Soc. Japan 30 (1978), 495–504.CrossRefGoogle Scholar
[11]Kaliszewski, S. and Quigg, J., ‘Imprimitivity for C*-coactions of non-amenable groups’, Math. Proc. Cambridge Philos. Soc. 123 (1998), 101–118.CrossRefGoogle Scholar
[12]Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Duality of restriction and induction for C*-coactions’, Trans. Amer. Math. Soc. 349 (1997), 2085–2113.CrossRefGoogle Scholar
[13]Katayama, Y., ‘Takesaki's duality for a non-degenerate co-action’, Math. Scand. 55 (1985), 141–151.CrossRefGoogle Scholar
[14]Lance, E.C., Hilbert C*-modules, London Math. Soc. Lecture Note Ser. 210 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
[15]Mansfield, K., ‘Induced representations of crossed products by coactions’, J. Funct. Anal. 97 (1991), 112–161.CrossRefGoogle Scholar
[16]Ng, C.K., ‘Coactions and crossed products of Hopf C*-algebras II: Hilbert C*-modules’, (preprint, 1995).Google Scholar
[17]Ng, C.K., ‘Coactions and crossed products of Hopf C*-algebras’, Proc. London Math. Soc. 72 (1996), 638–659.CrossRefGoogle Scholar
[18]Ng, C.K., ‘Morita equivalences between fixed point algebras and crossed products’, Proc. Cambridge Philos. Soc. 125 (1999), 43–52.CrossRefGoogle Scholar
[19]Ng, C.K., ‘Morphisms of multiplicative unitaries’, J. Operator Theory 38 (1997), 203–224.Google Scholar
[20]Nilsen, M., ‘Duality for crossed products of C*-algebras by non-amenable groups’, Proc. Amer. Math. Soc. 126 (1998), 2969–2978.CrossRefGoogle Scholar
[21]Rieffel, M.A., ‘Induced representations of C*-algebras’, Adv. Math. 13 (1974), 176–257.CrossRefGoogle Scholar
[22]Watatani, Y., ‘Index for C*-subalgebras’, Mem. Amer. Math. Soc. 83 (1990), pp. 117.Google Scholar