Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T19:32:21.175Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVALENCE OF SEMI-NORMS RELATED TO SUPER WEAKLY COMPACT OPERATORS

Part of: General theory of linear operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  22 June 2021

KUN TU Open the ORCID record for KUN TU [Opens in a new window]
KUN TU*
Affiliation:
School of Mathematical Sciences, Yangzhou University, Siwangting Road No. 180, Yangzhou 225002, Jiangsu, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study super weakly compact operators through a quantitative method. We introduce a semi-norm 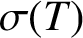$\sigma (T)$ of an operator 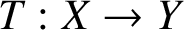$T:X\to Y$ , where X, Y are Banach spaces, the so-called measure of super weak noncompactness, which measures how far T is from the family of super weakly compact operators. We study the equivalence of the measure 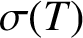$\sigma (T)$ and the super weak essential norm of T. We prove that Y has the super weakly compact approximation property if and and only if these two semi-norms are equivalent. As an application, we construct an example to show that the measures of T and its dual 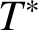$T^*$ are not always equivalent. In addition we give some sequence spaces as examples of Banach spaces having the super weakly compact approximation property.

Keywords

measure of super weak noncompactnesssuper weakly compact approximationsuper weak compact operators

MSC classification

Primary: 47A30: Norms (inequalities, more than one norm, etc.)
Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 506 - 518
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by NSFC, grant no. 11701501, and funding from Yangzhou University.

References

Astala, K., ‘On Measures of Noncompactness and Ideal Variations in Banach Spaces’, Ann. Acad. Sci. Fenn. Math. Diss. 29 (1980), 42 pages.Google Scholar
Astala, K. and Tylli, H.-O., ‘On the bounded compact approximation property and measures of noncompactness’, J. Funct. Anal. 70(2) (1987), 388–401.CrossRefGoogle Scholar
Astala, K. and Tylli, H.-O., ‘Seminorms related to weak compactness and to Tauberian operators’, Math. Proc. Cambridge Philos. Soc. 107(2) (1990), 367–375.10.1017/S0305004100068638CrossRefGoogle Scholar
Beauzamy, B., ‘Opérateurs uniformément convexifiants’, Studia Math. 57(2) (1976), 103–139.10.4064/sm-57-2-103-139CrossRefGoogle Scholar
Cheng, L., Cheng, Q., Luo, S., Tu, K. and Zhang, J., ‘On super weak compactness of subsets and its equivalences in Banach spaces’, J. Convex Anal. 25(3) (2018), 899–926.Google Scholar
Cheng, L., Cheng, Q., Wang, B. and Zhang, W., ‘On super-weakly compact sets and uniformly convexifiable sets’, Studia Math. 199(2) (2010), 145–169.10.4064/sm199-2-2CrossRefGoogle Scholar
Enflo, P., ‘Banach spaces which can be given an equivalent uniformly convex norm’, Israel J. Math. 13 (1972), 281–288.CrossRefGoogle Scholar
Goldenstein, L. S. and Markus, A. S., ‘On a measure of noncompactness of bounded sets and linear operators’, in: Studies in Algebra and Mathematical Analysis (Karta Moldovenjaski, Kishinev, 1965), 45–54.Google Scholar
González, M. and Abejón, A. M., Tauberian Operators , Operator Theory: Advances and Applications, 194 (Birkhäuser, Basel, 2010).CrossRefGoogle Scholar
James, R. C., ‘Some self-dual properties of normed linear spaces’, in: Sympos. Infinite-Dimensional Topology (Louisiana State University, Baton Rouge, LA, 1967), Annals of Mathematics Studies, 69 (ed. Anderson, B. D.) (Princeton University Press, Princeton, NJ, 1972), 159–175.10.1515/9781400881406-016CrossRefGoogle Scholar
Kacena, M., Kalenda, O. F. K. and Spurny, J., ‘Quantitative Dunford–Pettis property’, Adv. Math. 234 (2013), 488–527.CrossRefGoogle Scholar
Kryczka, A., Prus, S. and Szczepanik, M., ‘Measure of weak noncompactness and real interpolation of operators’, Bull. Aust. Math. Soc. 62(3) (2000), 389–401 . CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. I. Sequence Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, 92 (Springer, Berlin–New York, 1977).Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. II. Function Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, 97 (Springer, Berlin–New York, 1979).CrossRefGoogle Scholar
Odell, E. and Tylli, H.-O., ‘Weakly compact approximation in Banach spaces’, Trans. Amer. Math. Soc. 357(3) (2005), 1125–1159.10.1090/S0002-9947-04-03684-0CrossRefGoogle Scholar
Raja, M., ‘Finitely dentable functions, operators and sets’, J. Convex Anal. 15(2) (2008), 219–233.Google Scholar
Raja, M., ‘Super WCG Banach spaces’, J. Math. Anal. Appl. 439(1) (2016), 183–196.CrossRefGoogle Scholar
Saksman, E. and Tylli, H.-O., ‘New examples of weakly compact approximation in Banach spaces’, Ann. Acad. Sci. Fenn. Math. 33(2) (2008), 429–438.Google Scholar
Tu, K., ‘Convexification of super weakly compact sets and measure of super weak noncompactness’, Proc. Amer. Math. Soc. 149(6) (2021), 2531–2538.10.1090/proc/15393CrossRefGoogle Scholar
Tu, K., ‘Measure of super weak noncompactness in some Banach sequence spaces’, J. Math. Anal. Appl. 496(2) (2021), Article ID 124813, 11 pages.CrossRefGoogle Scholar
Tylli, H.-O., ‘The essential norm of an operator is not self-dual’, Israel J. Math. 91(1–3) (1995), 93–110.CrossRefGoogle Scholar