No CrossRef data available.
Article contents
ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER
Published online by Cambridge University Press: 15 August 2018
Abstract
We consider a curvature flow 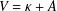 $V=\unicode[STIX]{x1D705}+A$ in a two-dimensional undulating cylinder
$V=\unicode[STIX]{x1D705}+A$ in a two-dimensional undulating cylinder 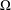 $\unicode[STIX]{x1D6FA}$ described by
$\unicode[STIX]{x1D6FA}$ described by 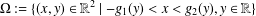 $\unicode[STIX]{x1D6FA}:=\{(x,y)\in \mathbb{R}^{2}\mid -g_{1}(y)<x<g_{2}(y),y\in \mathbb{R}\}$, where
$\unicode[STIX]{x1D6FA}:=\{(x,y)\in \mathbb{R}^{2}\mid -g_{1}(y)<x<g_{2}(y),y\in \mathbb{R}\}$, where 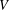 $V$ is the normal velocity of a moving curve contacting the boundaries of
$V$ is the normal velocity of a moving curve contacting the boundaries of 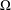 $\unicode[STIX]{x1D6FA}$ perpendicularly,
$\unicode[STIX]{x1D6FA}$ perpendicularly,  $\unicode[STIX]{x1D705}$ is its curvature,
$\unicode[STIX]{x1D705}$ is its curvature, 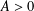 $A>0$ is a constant and
$A>0$ is a constant and 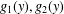 $g_{1}(y),g_{2}(y)$ are positive smooth functions. If
$g_{1}(y),g_{2}(y)$ are positive smooth functions. If 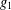 $g_{1}$ and
$g_{1}$ and 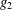 $g_{2}$ are periodic functions and there are no stationary curves, Matano et al. [‘Periodic traveling waves in a two-dimensional cylinder with saw-toothed boundary and their homogenization limit’, Netw. Heterog. Media1 (2006), 537–568] proved the existence of a periodic travelling wave. We consider the case where
$g_{2}$ are periodic functions and there are no stationary curves, Matano et al. [‘Periodic traveling waves in a two-dimensional cylinder with saw-toothed boundary and their homogenization limit’, Netw. Heterog. Media1 (2006), 537–568] proved the existence of a periodic travelling wave. We consider the case where 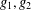 $g_{1},g_{2}$ are general nonperiodic positive functions and the problem has some stationary curves. For each stationary curve
$g_{1},g_{2}$ are general nonperiodic positive functions and the problem has some stationary curves. For each stationary curve 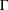 $\unicode[STIX]{x1D6E4}$ unstable from above/below, we construct an entire solution growing out of it, that is, a solution curve
$\unicode[STIX]{x1D6E4}$ unstable from above/below, we construct an entire solution growing out of it, that is, a solution curve 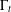 $\unicode[STIX]{x1D6E4}_{t}$ which increases/decreases monotonically, converging to
$\unicode[STIX]{x1D6E4}_{t}$ which increases/decreases monotonically, converging to 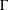 $\unicode[STIX]{x1D6E4}$ as
$\unicode[STIX]{x1D6E4}$ as 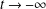 $t\rightarrow -\infty$ and converging to another stationary curve or to
$t\rightarrow -\infty$ and converging to another stationary curve or to 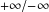 $+\infty /-\infty$ as
$+\infty /-\infty$ as 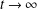 $t\rightarrow \infty$.
$t\rightarrow \infty$.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 137 - 147
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
This research was partly supported by Shanghai NSF in China (No. 17ZR1420900).


