Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T02:30:44.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Duality for generalized problems in complex programming

Published online by Cambridge University Press:  17 April 2009

D.G. Mahajan  and
M.N. Vartak
D.G. Mahajan
Affiliation:
Department of Mathematics, Indian Institute of Technology, Bombay, India.
M.N. Vartak
Affiliation:
Department of Mathematics, Indian Institute of Technology, Bombay, India.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Weak duality and direct duality theorems are proved, under appropriate assumptions, for the following pair of programming problems in complex space:

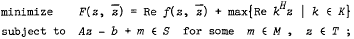
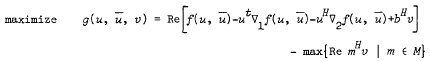
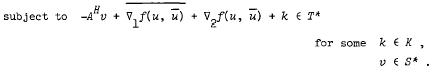
The objective function may be nondifferentiable and the constraints are of a more general nature than those considered earlier by various authors. Several well-known results are shown to be special cases of the results proved here.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 14 , Issue 1 , February 1976 , pp. 11 - 22
Copyright
Copyright © Australian Mathematical Society 1976

References

[1]Abrams, Robert A., “Nonlinear programming in complex space: sufficient conditions and duality”, J. Math. Anal. Appl. 38 (1972), 619–632.CrossRefGoogle Scholar
[2]Abrams, Robert A. and Ben-Israel, Adi, “A duality theorem for complex quadratic programming”, J. Optimization Theory Appl. 4 (1969), 244–252.CrossRefGoogle Scholar
[3]Ben-Israel, Adi, “Linear equations and inequalities on finite dimensional, real or complex, vector spaces: a unified theory”, J. Math. Anal. Appl. 27 (1969), 367–389.CrossRefGoogle Scholar
[4]Bhatia, Davinder and Kaul, R.N., “Nonlinear programming in complex space”, J. Math. Anal. Appl. 28 (1969), 144–152.CrossRefGoogle Scholar
[5]Hanson, Morgan A. and Mond, Bertram, “Quadratic programming in complex space”, J. Math. Anal. Appl. 20 (1967), 507–514.CrossRefGoogle Scholar
[6]Hanson, Morgan A. and Mond, Bertram, “Duality for nonlinear programming in complex space”, J. Math. Anal. Appl. 28 (1969), 52–58.CrossRefGoogle Scholar
[7]Levinson, Norman, “Linear programming in complex space”, J. Math. Anal. Appl. 14 (1966), 44–62.CrossRefGoogle Scholar
[8]Mahajan, D.G. and Vartak, M.N., “Symmetry and duality for a class of nonlinear programs in complex space”, submitted.Google Scholar
[9]Mond, Bertram, “Nonlinear nondifferentiable programming in complex space”, Nonlinear programming, 385–400.(Proc. Sympos. Mathematics Research Center, University of Wisconsin, Madison. Academic Press, New York, London, 1970).CrossRefGoogle Scholar
[10]Mond, B., “Nonlinear complex programming”, J. Math. Anal. Appl. 43 (1973), 633–641.CrossRefGoogle Scholar
[11]Mond, Bertram, “Duality for complex programming”, J. Math. Anal. Appl. 46 (1974), 478–486.CrossRefGoogle Scholar
[12]Mond, Bertram, “Duality for a complex nonlinear program”, Opsearch 11 (1974), 1–9.Google Scholar
[13]Rani, Oma, “A duality theorem for complex nonlinear programming”, Opsearoh 10 (1973), 14–23.Google Scholar
[14]Rani, Oma and Kaul, R.N., “Nonlinear programming in complex space”, J. Math. Anal. Appl. 43 (1973), 1–14.CrossRefGoogle Scholar
[15]Smiley, M.F., “Duality in complex homogeneous programming”, J. Math. Anal. Appl. 40 (1972), 153–158.CrossRefGoogle Scholar