Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T12:18:46.344Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DISTRIBUTIONAL 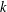$k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES

Part of: Linear function spaces and their duals Distributions, generalized functions, distribution spaces Elliptic equations and systems

Published online by Cambridge University Press:  23 October 2019

QIANG TU Open the ORCID record for QIANG TU [Opens in a new window] ,
WENYI CHEN Open the ORCID record for WENYI CHEN [Opens in a new window]  and
XUETING QIU Open the ORCID record for XUETING QIU [Opens in a new window]
QIANG TU*
Affiliation:
Faculty of Mathematics and Statistics,Hubei University, Wuhan, China email [email protected]
WENYI CHEN
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan, China email [email protected]
XUETING QIU
Affiliation:
Faculty of Mathematics and Statistics,Hubei University, Wuhan, China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of a distributional 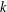$k$-Hessian (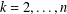$k=2,\ldots ,n$) associated with fractional Sobolev functions on $\unicode[STIX]{x1D6FA}$, a smooth bounded open subset in 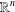$\mathbb{R}^{n}$. We show that the distributional 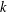$k$-Hessian is weakly continuous on the fractional Sobolev space 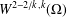$W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$ and that the weak continuity result is optimal, that is, the distributional 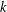$k$-Hessian is well defined in 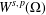$W^{s,p}(\unicode[STIX]{x1D6FA})$ if and only if 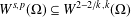$W^{s,p}(\unicode[STIX]{x1D6FA})\subseteq W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$.

Keywords

k-Hessianfractional Sobolev spacedistribution

MSC classification

Primary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Secondary: 35J60: Nonlinear elliptic equations 46F10: Operations with distributions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 496 - 507
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by Hubei Key Laboratory of Applied Mathematics, Hubei University.

References

Baer, E. and Jerison, D., ‘Optimal function spaces for continuity of the Hessian determinant as a distribution’, J. Funct. Anal. 269 (2015), 1482–1514.Google Scholar
Brezis, H. and Nguyen, H., ‘The Jacobian determinant revisited’, Invent. Math. 185 (2011), 17–54.Google Scholar
Colesanti, A. and Hug, D., ‘Hessian measures of semi-convex functions and applications to support measures of convex bodies’, Manuscripta Math. 101 (2000), 209–238.10.1007/s002290050015Google Scholar
Colesanti, A. and Salani, P., ‘Generalized solutions of Hessian equations’, Bull. Aust. Math. Soc. 56 (1997), 459–466.Google Scholar
Fu, J., ‘Monge–Ampère functions I’, Indiana Univ. Math. J. 38 (1989), 745–771.Google Scholar
Giaquinta, M., Modica, G. and Souček, J., Cartesian Currents in the Calculus of Variations, I (Springer, Berlin, 1998).Google Scholar
Iwaniec, T., ‘On the concept of the weak Jacobian and Hessian’, Papers on analysis: A volume dedicated to Olli Martio on the occasion of his 60th birthday, Rep. Univ. Jyväskylä Dep. Math. Stat. 83 (2001), 181–205.Google Scholar
Stein, E., ‘The characterization of functions arising as potentials. I’, Bull. Amer. Math. Soc. (N.S.) 67 (1961), 102–104.Google Scholar
Stein, E., ‘The characterization of functions arising as potentials. II’, Bull. Amer. Math. Soc. (N.S.) 68 (1962), 577–582.Google Scholar
Strichartz, R., ‘Fubini-type theorems’, Ann. Scuola Norm. Sup. Pisa (3) 22 (1968), 399–408.Google Scholar
Treibel, H., Theory of Functions Spaces, Monographs in Mathematics, 78 (Birkhauser Verlag, Basel, 1983).Google Scholar
Trudinger, N. and Wang, X., ‘Hessian measures I’, Topol. Methods Nonlinear Anal. 10 (1997), 225–239.Google Scholar
Trudinger, N. and Wang, X., ‘Hessian measures II’, Ann. of Math. (2) 150 (1999), 579–604.Google Scholar