Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-13T20:34:39.847Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTION OF r-FREE INTEGERS OVER A FLOOR FUNCTION SET

Part of: Multiplicative number theory

Published online by Cambridge University Press:  23 November 2022

PINTHIRA TANGSUPPHATHAWAT Open the ORCID record for PINTHIRA TANGSUPPHATHAWAT [Opens in a new window] ,
TEERAPAT SRICHAN Open the ORCID record for TEERAPAT SRICHAN [Opens in a new window]  and
VICHIAN LAOHAKOSOL Open the ORCID record for VICHIAN LAOHAKOSOL [Opens in a new window]
PINTHIRA TANGSUPPHATHAWAT
Affiliation:
Department of Mathematics, Faculty of Science and Technology, Phranakhon Rajabhat University, Bangkok 10220, Thailand e-mail: [email protected]
TEERAPAT SRICHAN*
Affiliation:
Department of Mathematics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand
VICHIAN LAOHAKOSOL
Affiliation:
Department of Mathematics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a positive integer 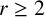$r\geq 2$, a natural number n is r-free if there is no prime p such that 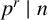$p^r\mid n$. Asymptotic formulae for the distribution of r-free integers in the floor function set 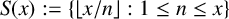$S(x):=\{\lfloor x/ n \rfloor :1\leq n\leq x\}$ are derived. The first formula uses an estimate for elements of 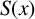$S(x)$ belonging to arithmetic progressions. The other, more refined, formula makes use of an exponent pair and the Riemann hypothesis.

Keywords

floor functionr-free integer

MSC classification

Primary: 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Secondary: 11N69: Distribution of integers in special residue classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 107 - 113
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was financially supported by the Office of the Permanent Secretary, Ministry of Higher Education, Science, Research and Innovation, Grant No. RGNS 63-40.

References

Abercrombie, A. G., Banks, W. D. and Shparlinski, I. E., ‘Arithmetic functions on Beatty sequences’, Acta Arith. 136 (2009), 81–89.CrossRefGoogle Scholar
Apostol, T. M., Introduction to Analytic Number Theory (Springer, New York, 1976).Google Scholar
Bordellés, O., ‘On certain sums of number theory’, Int. J. Number Theory 18(9) (2022), 2053–2074.CrossRefGoogle Scholar
Bordellés, O., Dai, L., Heyman, R., Pan, H. and Shparlinski, I. E., ‘On a sum involving the Euler function’, J. Number Theory 202 (2019), 278–297.CrossRefGoogle Scholar
Cao, X. D. and Zhai, W. G., ‘ The distribution of square-free numbers of the form $\left\lfloor {n}^c\right\rfloor$ ’, J. Théor. Nombres Bordeaux 10(2) (1998), 287–299.CrossRefGoogle Scholar
Cao, X. D. and Zhai, W. G., ‘On the distribution of square-free numbers of the form $\left\lfloor {n}^c\right\rfloor$ (II)’, Acta Math. Sinica (Chin. Ser.) 51 (2008), 1187–1194.Google Scholar
Deshouillers, J. M., ‘A remark on cube-free numbers in Segal–Piatetski-Shapiro sequences’, Hardy-Ramanujan J. 41 (2019), 127–132.Google Scholar
Goryashin, D. V., ‘ Squarefree numbers in the sequence $\left\lfloor \alpha {n}\right\rfloor$ ’, Chebyshevskiĭ Sb. 14(3) (2013), 42–48.Google Scholar
Gűloğlu, A. M. and Nevans, C. W., ‘Sums of multiplicative functions over a Beatty sequence’, Bull. Aust. Math. Soc. 78 (2008), 327–334.CrossRefGoogle Scholar
Heyman, R., ‘Cardinality of a floor function set’, Integers 19 (2019), Article no. A67.Google Scholar
Ivić, A., The Theory of the Riemann Zeta Function (Wiley, New York, 1985).Google Scholar
Liu, K., Wu, J. and Yang, Z.-S., ‘On some sums involving the integral part function’, Preprint, 2021, arXiv:2109.01382v1.Google Scholar
Rieger, G. J., ‘Remark on a paper of Stux concerning squarefree numbers in non-linear sequences’, Pacific J. Math. 78(1) (1978), 241–242.CrossRefGoogle Scholar
Srichan, T., ‘On the distribution of $\left(k,r\right)$ -integers in Piatetski-Shapiro sequences’, Czechoslovak Math. J. 71(4) (2021), 1063–1070.CrossRefGoogle Scholar
Srichan, T., ‘Multiplicative functions of special type on Piatetski-Shapiro sequences’, Math. Slovaca 72(5) (2022), 1145–1150.CrossRefGoogle Scholar
Stucky, J., ‘The fractional sum of small arithmetic functions’, J. Number Theory 238 (2022), 731–739.CrossRefGoogle Scholar
Stux, I. E., ‘Distribution of squarefree integers in non-linear sequences’, Pacific J. Math. 59(2) (1975), 577–584.CrossRefGoogle Scholar
Tangsupphathawat, P., Srichan, T. and Laohakosol, V., ‘Consecutive square-free numbers in Piatetski-Shapiro sequences’, Bull. Aust. Math. Soc. 105(2) (2022), 217–222.CrossRefGoogle Scholar
Veasna, K., Srichan, T. and Mavecha, S., ‘On $r$ -free integers in Beatty sequences’, Bol. Soc. Mat. Mex. (3) 28(2) (2022), 1–10.Google Scholar
Yu, Y. and Wu, J., ‘Distribution of elements of a floor function set in arithmetical progressions’, Bull. Aust. Math. Soc., to appear. Published online (1 March 2022).CrossRefGoogle Scholar
Zhang, M. and Jinjiang, L., ‘ Distribution of cube-free numbers with form $\left[{n}^c\right]$ ’, Front. Math. China 12(6) (2017), 1515–1525.CrossRefGoogle Scholar
Zhang, W., ‘On general sums involving the floor function with applications to $k$ -free numbers’, Preprint, 2021, arXiv:2112.06156.Google Scholar