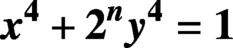Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-16T07:20:59.267Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIOPHANTINE EQUATION $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS

Part of: Algebraic number theory: global fields Diophantine equations

Published online by Cambridge University Press:  06 November 2020

ANDREW LI Open the ORCID record for ANDREW LI [Opens in a new window]
ANDREW LI*
Affiliation:
Department of Mathematics, University of Nebraska Omaha, Omaha, NE68182, USA
*
e-mail: ali01@unomaha.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Aigner showed in 1934 that nontrivial quadratic solutions to 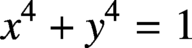$x^4 + y^4 = 1$ exist only in 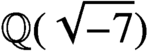$\mathbb Q(\sqrt {-7})$ . Following a method of Mordell, we show that nontrivial quadratic solutions to 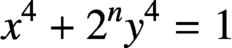$x^4 + 2^ny^4 = 1$ arise from integer solutions to the equations 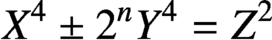$X^4 \pm 2^nY^4 = Z^2$ investigated in 1853 by V. A. Lebesgue.

Keywords

quartic Diophantine equationsquadratic number fields

MSC classification

Primary: 11D25: Cubic and quartic equations
Secondary: 11R11: Quadratic extensions 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 21 - 28
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aigner, A., ‘Über die möglichkeit von ${x}^4+{y}^4={z}^4$ in quadratischen körpern’, Jahresber. Dtsch. Math.-Ver. 43 (1934), 226–229.Google Scholar
Faddeev, D. K., ‘Group of divisor classes on the curve defined by the equation ${x}^4+{y}^4=1$ ’, Soviet Math. Dokl. 1 (1960), 1149–1151.Google Scholar
Lebesgue, V. A., ‘Résolution des équations biquadratiques (1), (2) ${z}^2={x}^4\pm {2}^m{y}^4$ , (3) ${z}^2={2}^m{x}^4-{y}^4$ , (4), (5) ${2}^m{z}^2={x}^4\pm {y}^4$ ’, J. Math. Pures Appl. 18 (1853), 73–86. https://archive.org/details/s1journaldemat18liou/page/72/mode/2up.Google Scholar
Manley, E. D., ‘On quadratic solutions of ${x}^4+p{y}^4={z}^4$ ’, Rocky Mountain J. Math. 36(3) (2006), 1027–1031.Google Scholar
Mordell, L. J., ‘The Diophantine equation ${x}^4+{y}^4=1$ in algebraic number fields’, Acta Arith. 14 (1967/68), 347–355.CrossRefGoogle Scholar
The LMFDB Collaboration, ‘The L-functions and modular forms database’, http://www.lmfdb.org, (online; accessed 28 July 2020). Google Scholar