Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T12:45:13.492Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIMENSION OF CENTRALISERS OF MATRICES OF ORDER $n$

Part of: Combinatorics

Published online by Cambridge University Press:  26 September 2016

DONG ZHANG  and
HANCONG ZHAO
DONG ZHANG
Affiliation:
LMAM and School of Mathematical Sciences, Peking University, Beijing 100871, China email [email protected], [email protected]
HANCONG ZHAO*
Affiliation:
LMAM and School of Mathematical Sciences, Peking University, Beijing 100871, China email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the integer sequence 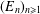$(E_{n})_{n\geq 1}$ , where 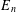$E_{n}$ counts the number of possible dimensions for centralisers of 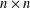$n\times n$ matrices. We give an example to show another combinatorial interpretation of 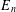$E_{n}$ and present an implicit recurrence formula for 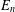$E_{n}$ , which may provide a fast algorithm for computing 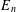$E_{n}$ . Based on the recurrence, we obtain the asymptotic formula $E_{n}=\frac{1}{2}n^{2}-\frac{2}{3}\sqrt{2}n^{3/2}+O(n^{5/4})$ .

Keywords

centraliserasymptotic enumerationpartitioncommutator

MSC classification

Primary: 05A05: Permutations, words, matrices
Secondary: 05A16: Asymptotic enumeration 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 353 - 361
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Brouder, C., Keith, W. J. and Mestre, A., ‘Several graph sequences as solutions of a double recurrence’, J. Comb. Number Theory 6(2) (2015), 37–51.Google Scholar
Hardy, G. H. and Ramanujan, S., ‘Asymptotic formulae in combinatory analysis’, Proc. Lond. Math. Soc. (3) 17 (1918), 75–115.Google Scholar
O’Donovan, B., ‘The action of generalised symmetric groups on symmetric and exterior powers of their natural representations’, Preprint, 2015, arXiv:1506.00184.Google Scholar
O’Meara, K. C., Clark, J. and Vinsonhaler, C. I., Advanced Topics in Linear Algebra (Oxford University Press, New York, 2011).Google Scholar
Online Encyclopaedia of Integer Sequences A000124, http://oeis.org/A000124.Google Scholar
Online Encyclopaedia of Integer Sequences A069999, http://oeis.org/A069999.Google Scholar
Savitt, D. and Stanley, R. P., ‘A note on the symmetric powers of the standard representation of S n ’, Electron. J. Combin. 7 (2000), Research Paper #R6, 8 pp.Google Scholar