Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-17T14:32:39.628Z Has data issue: false hasContentIssue false
  • English
  • Français

DETERMINING CROSSING NUMBERS OF GRAPHS OF ORDER SIX USING CYCLIC PERMUTATIONS

Part of: Graph theory

Published online by Cambridge University Press:  17 August 2018

MICHAL STAŠ Open the ORCID record for MICHAL STAŠ [Opens in a new window]
MICHAL STAŠ*
Affiliation:
Department of Mathematics and Theoretical Informatics, Faculty of Electrical Engineering and Informatics, Technical University of Košice, Letná 9, 042 00 Košice, Slovak Republic email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend known results concerning crossing numbers by giving the crossing number of the join product 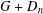$G+D_{n}$, where the connected graph 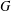$G$ consists of one 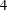$4$-cycle and of two leaves incident with the same vertex of the 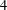$4$-cycle, and 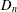$D_{n}$ consists of $n$ isolated vertices. The proofs are done with the help of software that generates all cyclic permutations for a given number 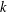$k$ and creates a graph for calculating the distances between all 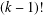$(k-1)!$ vertices of the graph.

Keywords

graphdrawingcrossing numberjoin productrotation

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Secondary: 05C38: Paths and cycles
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 353 - 362
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The research was supported by the internal faculty research project no. FEI-2017-39.

References

Berežný, Š., Buša, J. Jr and Staš, M., ‘Software solution of the algorithm of the cyclic-order graph’, Acta Electrotech. Inform. 18(1) (2018), 3–10.Google Scholar
Berežný, Š. and Staš, M., ‘On the crossing number of the join of five vertex graph G with the discrete graph D n ’, Acta Electrotech. Inform. 17(3) (2017), 27–32.Google Scholar
Berežný, Š. and Staš, M., ‘Cyclic permutations and crossing numbers of join products of symmetric graph of order six’, Carpathian J. Math. 34(2) (2018), 143–155.Google Scholar
Hernández-Vélez, C., Medina, C. and Salazar, G., ‘The optimal drawing of K 5, n ’, Electron. J. Combin. 21(4) (2014), P4.1, 29 pages.Google Scholar
Kleitman, D. J., ‘The crossing number of K 5, n ’, J. Combin. Theory 9 (1970), 315–323.Google Scholar
Klešč, M., ‘The join of graphs and crossing numbers’, Electron. Notes Discrete Math. 28 (2007), 349–355.Google Scholar
Klešč, M., ‘The crossing number of join of the special graph on six vertices with path and cycle’, Discrete Math. 310 (2010), 1475–1481.Google Scholar
Klešč, M., Petrillová, J. and Valo, M., ‘On the crossing numbers of Cartesian products of wheels and trees’, Discuss. Math. Graph Theory 71 (2017), 339–413.Google Scholar
Klešč, M. and Schrötter, Š., ‘The crossing numbers of join products of paths with graphs of order four’, Discuss. Math. Graph Theory 31 (2011), 312–331.Google Scholar
Klešč, M. and Schrötter, Š., ‘The crossing numbers of join of paths and cycles with two graphs of order five’, in: Mathematical Modeling and Computational Science, Lecture Notes in Computer Science, 7125 (Springer, Berlin–Heidelberg, 2012), 160–167.Google Scholar
Staš, M., ‘On the crossing number of the join of the discrete graph with one graph of order five’, Math. Model. Geom. 5(2) (2017), 12–19.Google Scholar
Staš, M., ‘Cyclic permutations: crossing numbers of the join products of graphs’, in: Proc. APLIMAT 2018: 17th Conf. Applied Mathematics (Slovak University of Technology, Bratislava, 2018), 979–987.Google Scholar
Woodall, D. R., ‘Cyclic-order graphs and Zarankiewicz’s crossing number conjecture’, J. Graph Theory 17 (1993), 657–671.Google Scholar