Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T22:36:49.337Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREES OF BRAUER CHARACTERS AND NORMAL SYLOW 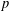$p$-SUBGROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  08 January 2020

XIAOYOU CHEN Open the ORCID record for XIAOYOU CHEN [Opens in a new window]  and
MARK L. LEWIS Open the ORCID record for MARK L. LEWIS [Opens in a new window]
XIAOYOU CHEN
Affiliation:
College of Science, Henan University of Technology, Zhengzhou450001, China email [email protected]
MARK L. LEWIS*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 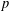$p$ be a prime, 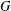$G$ a solvable group and 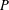$P$ a Sylow 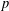$p$-subgroup of 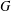$G$. We prove that 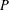$P$ is normal in 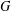$G$ if and only if 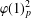$\unicode[STIX]{x1D711}(1)_{p}^{2}$ divides 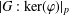$|G:\ker (\unicode[STIX]{x1D711})|_{p}$ for all monomial monolithic irreducible 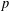$p$-Brauer characters 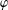$\unicode[STIX]{x1D711}$ of 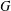$G$.

Keywords

Brauer charactermonomial charactercharacter degreeSylow subgroup

MSC classification

Primary: 20C20: Modular representations and characters
Secondary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 237 - 239
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, X., Cossey, J. P., Lewis, M. L. and Tong-Viet, H. P., ‘Blocks of small defect in alternating groups and squares of Brauer character degrees’, J. Group Theory 20 (2017), 1155–1173.CrossRefGoogle Scholar
Chen, X. and Lewis, M. L., ‘Squares of degrees of Brauer characters and monomial Brauer characters’, Bull. Aust. Math. Soc. 100 (2019), 58–60.CrossRefGoogle Scholar
Chen, X. and Lewis, M. L., ‘Monolithic Brauer characters’, Bull. Aust. Math. Soc. 100 (2019), 434–439.CrossRefGoogle Scholar
Gallagher, P. X., ‘Group characters and normal Hall subgroups’, Nagoya Math. J. 21 (1962), 223–230.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Isaacs, I. M., ‘Large orbits in actions of nilpotent groups’, Proc. Amer. Math. Soc. 127 (1999), 45–50.CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Tong-Viet, H. P., ‘Brauer characters and normal Sylow p-subgroups’, J. Algebra 503 (2018), 265–276; ‘Corrigendum to “Brauer characters and normal Sylow $p$-subgroups”’, J. Algebra 505 (2018), 597–598.CrossRefGoogle Scholar