Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T15:43:36.304Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DEGREE OF HOLOMORPHIC APPROXIMATION ON A TOTALLY REAL SET

Part of: Holomorphic convexity

Published online by Cambridge University Press:  09 February 2009

SAID ASSERDA
SAID ASSERDA*
Affiliation:
Université Ibn Tofail, Faculté des Sciences, Departement des Mathématiques, BP 242, Kénitra, Morocco (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a totally real set on a Stein open set Ω on a complete noncompact Kähler manifold (M,g) with nonnegative holomorphic bisectional curvature such that (Ω,g) has bounded geometry at E. Then every function f in a Cp class with compact support on Ω and 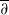-flat on E up to order p−1,p≥2 (respectively, in a Gevrey class of order s>1, with compact support on Ω and 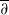-flat on E up to infinite order) can be approximated on compacts subsets of E by holomorphic functions fk on Ω with degree of approximation equal k−p/2 (respectively, exp (−c(s)k1/2(s−1)) ).

Keywords

totally real setdegree of approximation∂ operator

MSC classification

Secondary: 32E30: Holomorphic and polynomial approximation, Runge pairs, interpolation
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 1 , February 2009 , pp. 171 - 176
Copyright
Copyright © Australian Mathematical Society 2009

References

[1] Berndtsson, B., ‘A remark on approximation on totally real sets’, arxiv:math/0608058v.1, 2006 and arxiv:math/06080582v.2, 2008.Google Scholar
[2] Chen, B.-L., Fu, X.-Y., Yin, L. and Zhu, X.-P., ‘Sharp dimension estimates of holomorphic functions and rigidity’, Trans. Amer. Math. Soc. 385(4) (2006), 1435–1454.Google Scholar
[3] Cheng, S. Y. and Yau, S. T., ‘On the existence of a complete Kähler metric on noncompact complex manifolds and regularity of Fefferman’s equations’, Comm. Pure Appl. Math. 33 (1980), 507–544.CrossRefGoogle Scholar
[4] Delin, H., ‘Pontwise estimates for the weighted Bergmann projection kernel in ℂn, using a weighted L 2 estimates for the -equation’, Ann. Inst. Fourier 48(4) (1998), 967–997.CrossRefGoogle Scholar
[5] Demailly, J. P., ‘Estimations L 2 pour l’operateur d-bar d’un fibré vectoriel holomorphe semi-positif au dessus d’une variété Kählerienne complète’, Ann. Sci. Ecole Norm. Sup 4e Sér. 15 (1982), 457–511.Google Scholar
[6] Hörmander, L. and Wermer, J., ‘Uniform approximation on compacts set in ℂn’, Math. Scand. 23 (1968), 5–21.CrossRefGoogle Scholar
[7] Wermer, J., Banach Algebras and Several Complex Variables, 2nd edn (Springer, Berlin, 1976).CrossRefGoogle Scholar