Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:17:27.239Z Has data issue: false hasContentIssue false
  • English
  • Français

CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS

Part of: Real and complex fields Algebraic number theory: global fields Combinatorics General field theory

Published online by Cambridge University Press:  28 March 2019

BISWAJIT KOLEY Open the ORCID record for BISWAJIT KOLEY [Opens in a new window]  and
SATYANARAYANA REDDY ARIKATLA Open the ORCID record for SATYANARAYANA REDDY ARIKATLA [Opens in a new window]
BISWAJIT KOLEY
Affiliation:
Department of Mathematics, Shiv Nadar University, 201314, India email [email protected]
SATYANARAYANA REDDY ARIKATLA*
Affiliation:
Department of Mathematics, Shiv Nadar University, 201314, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A cyclotomic polynomial 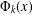$\unicode[STIX]{x1D6F7}_{k}(x)$ is an essential cyclotomic factor of 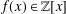$f(x)\in \mathbb{Z}[x]$ if 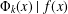$\unicode[STIX]{x1D6F7}_{k}(x)\mid f(x)$ and every prime divisor of 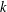$k$ is less than or equal to the number of terms of 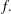$f.$ We show that if a monic polynomial with coefficients from 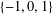$\{-1,0,1\}$ has a cyclotomic factor, then it has an essential cyclotomic factor. We use this result to prove a conjecture posed by Mercer [‘Newman polynomials, reducibility, and roots on the unit circle’, Integers12(4) (2012), 503–519].

Keywords

Newman polynomialscyclotomic polynomialsirreducible polynomials

MSC classification

Primary: 11R09: Polynomials (irreducibility, etc.)
Secondary: 05A17: Partitions of integers 12D05: Polynomials 12E05: Polynomials (irreducibility, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 41 - 47
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

de Bruijn, N. G., ‘On the factorization of cyclic groups’, Indag. Math. 15 (1953), 370–377.10.1016/S1385-7258(53)50046-0Google Scholar
Dresden, G., ‘Resultants of cyclotomic polynomials’, Rocky Mountain J. Math. 42 (2012), 1461–1469.10.1216/RMJ-2012-42-5-1461Google Scholar
Drungilas, P., Jankauskas, J. and S̆iurys, J., ‘On Littlewood and Newman polynomial multiples of Borwein polynomials’, Math. Comput. 87(311) (2018), 1523–1541.10.1090/mcom/3258Google Scholar
Filaseta, M. and Solan, J., ‘An extension of a theorem of Ljunggren’, Math. Scand. 84(1) (1999), 5–10.10.7146/math.scand.a-13928Google Scholar
Finch, C. and Jones, L., ‘On the irreducibility of { - 1, 0, 1}-quadrinomials’, Integers 6 (2006), A16, 4 pages.Google Scholar
Lam, T. Y. and Leung, K. H., ‘On vanishing sums of roots of unity’, J. Algebra 224 (2000), 91–109.10.1006/jabr.1999.8089Google Scholar
Ljunggren, W., ‘On the irreducibility of certain trinomials and quadrinomials’, Math. Scand. 8 (1960), 65–70.10.7146/math.scand.a-10593Google Scholar
Mercer, I., ‘Newman polynomials, reducibility, and roots on the unit circle’, Integers 12(4) (2012), 503–519.10.1515/integers-2011-0120Google Scholar
Mills, W. H., ‘The factorization of certain quadrinomials’, Math. Scand. 57 (1985), 44–50.10.7146/math.scand.a-12105Google Scholar
Odlyzko, A. M. and Poonen, B., ‘Zeros of polynomials with 0, 1 coefficients’, Enseign. Math. 39 (1993), 317–348.Google Scholar
Reddy, A. S., ‘The lowest degree $0,1$ -polynomial divisible by cyclotomic polynomial’, Preprint, arXiv:1106.1271.Google Scholar
Selmer, E. S., ‘On the irreducibility of certain trinomials’, Math. Scand. 4 (1956), 287–302.10.7146/math.scand.a-10478Google Scholar
Tverberg, H., ‘On the irreducibility of the trinomials x n ± x m ± 1’, Math. Scand. 8 (1960), 121–126.10.7146/math.scand.a-10599Google Scholar