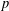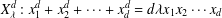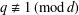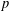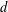Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McCarthy, Dermot
2017.
The number of
-points on Dwork hypersurfaces and hypergeometric functions.
Research in the Mathematical Sciences,
Vol. 4,
Issue. 1,
Barman, Rupam
and
Saikia, Neelam
2018.
Summation identities and transformations for hypergeometric series.
Annales mathématiques du Québec,
Vol. 42,
Issue. 2,
p.
133.
McCarthy, Dermot
2024.
The number of 𝔽q-points on diagonal
hypersurfaces with monomial deformation.
Pacific Journal of Mathematics,
Vol. 328,
Issue. 2,
p.
339.
Sulakashna
and
Barman, Rupam
2024.
Number of 𝔽q-points on diagonal hypersurfaces and hypergeometric function.
International Journal of Number Theory,
Vol. 20,
Issue. 10,
p.
2575.