Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T16:07:59.603Z Has data issue: false hasContentIssue false
  • English
  • Français

COUNTING CONJUGACY CLASSES IN 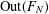$\text{Out}(F_{N})$

Part of: Dynamical systems with hyperbolic behavior Topological dynamics Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  28 March 2018

MICHAEL HULL Open the ORCID record for MICHAEL HULL [Opens in a new window]  and
ILYA KAPOVICH Open the ORCID record for ILYA KAPOVICH [Opens in a new window]
MICHAEL HULL
Affiliation:
Department of Mathematics, University of Florida, Box 118105, Gainesville, FL 32611-8105, USA email [email protected]
ILYA KAPOVICH*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Urbana, IL 61801, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if a finitely generated group 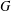$G$ has a nonelementary WPD action on a hyperbolic metric space 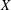$X$, then the number of 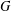$G$-conjugacy classes of 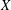$X$-loxodromic elements of 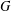$G$ coming from a ball of radius 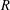$R$ in the Cayley graph of 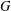$G$ grows exponentially in 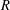$R$. As an application we prove that for 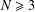$N\geq 3$ the number of distinct 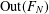$\text{Out}(F_{N})$-conjugacy classes of fully irreducible elements 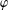$\unicode[STIX]{x1D719}$ from an 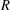$R$-ball in the Cayley graph of 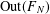$\text{Out}(F_{N})$ with 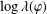$\log \unicode[STIX]{x1D706}(\unicode[STIX]{x1D719})$ of the order of 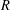$R$ grows exponentially in 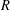$R$.

Keywords

free group automorphismsstretch factorsloxodromic elements

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 57M15: Relations with graph theory 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 412 - 421
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author was supported by the individual NSF grants DMS-1405146 and DMS-1710868. Both authors acknowledge the support of the conference grant DMS-1719710 ‘Conference on Groups and Computation’.

References

Algom-Kfir, Y. and Bestvina, M., ‘Asymmetry of Outer space’, Geom. Dedicata 156 (2012), 81–92.Google Scholar
Antolin, Y., Mj, M., Sisto, A. and Taylor, S. J., ‘Intersection properties of stable subgroups and bounded cohomology’, Indiana University Math. J., to appear, arXiv:1612.07227.Google Scholar
Aougab, T., Durham, M. G. and Taylor, S. J., ‘Pulling back stability with applications to Out(F n ) and relatively hyperbolic groups’, J. London Math. Soc. 96 (2017), 565–583.Google Scholar
Bestvina, M., ‘Geometry of Outer space’, in: Geometric Group Theory, IAS/Park City Mathematics Series, 21 (American Mathematical Society, Providence, RI, 2014), 173–206.CrossRefGoogle Scholar
Bestvina, M. and Feighn, M., ‘Hyperbolicity of the complex of free factors’, Adv. Math. 256 (2014), 104–155.Google Scholar
Bestvina, M. and Handel, M., ‘Train tracks and automorphisms of free groups’, Ann. of Math. 135 (1992), 1–51.Google Scholar
Coulbois, T. and Hilion, A., ‘Botany of irreducible automorphisms of free groups’, Pacific J. Math. 256(2) (2012), 291–307.Google Scholar
Coulbois, T. and Lustig, M., ‘Index realization for automorphisms of free groups’, Illinois J. Math. 59(4) (2015), 1111–1128.Google Scholar
Culler, M. and Vogtmann, K., ‘Moduli of graphs and automorphisms of free groups’, Invent. Math. 84(1) (1986), 91–119.CrossRefGoogle Scholar
Dahmani, F., Guirardel, V. and Osin, D., ‘Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces’, Mem. Amer. Math. Soc. 245 (2017), no. 1156.Google Scholar
Dowdall, S. and Taylor, S. J., ‘Hyperbolic extensions of free groups’, Geom. Topol. 22(1) (2018), 517–570.Google Scholar
Eskin, A. and Mirzakhani, M., ‘Counting closed geodesics in moduli space’, J. Mod. Dyn. 5(1) (2011), 71–105.CrossRefGoogle Scholar
Francaviglia, S. and Martino, A., ‘Metric properties of Outer space’, Publ. Mat. 55(2) (2011), 433–473.CrossRefGoogle Scholar
Handel, M. and Mosher, L., ‘The expansion factors of an outer automorphism and its inverse’, Trans. Amer. Math. Soc. 359 (2007), 3185–3208.CrossRefGoogle Scholar
Handel, M. and Mosher, L., ‘Axes in Outer space’, Mem. Amer. Math. Soc. 213 (2011), no. 1004.Google Scholar
Hull, M., ‘Small cancellation in acylindrically hyperbolic groups’, Groups Geom. Dynam. 10(4) (2016), 1077–1119.Google Scholar
Hull, M. and Osin, D., ‘Conjugacy growth of finitely generated groups’, Adv. Math. 235 (2013), 361–389.Google Scholar
Kapovich, I., ‘Algorithmic detectability of iwip automorphisms’, Bull. Lond. Math. Soc. 46(2) (2014), 279–290.Google Scholar
Kapovich, I. and Bell, M., ‘Detecting fully irreducible automorphisms: Q polynomial time algorithm’, Exp. Math. ; doi:10.1080/10586458.2017.1326326.Google Scholar
Margulis, G. A., On Some Aspects of the Theory of Anosov Systems, Springer Monographs in Mathematics (Springer, Berlin, 2004).Google Scholar
Osin, D., ‘Acylindrically hyperbolic groups’, Trans. Amer. Math. Soc. 368(2) (2016), 851–888.Google Scholar
Pfaff, C., ‘Ideal Whitehead graphs in Out(F r ). I. Some unachieved graphs’, New York J. Math. 21 (2015), 417–463.Google Scholar
Yang, W., ‘Statistically convex-cocompact actions of groups with contracting elements’, Preprint, 2016, arXiv:1612.03648.Google Scholar
Yang, W., ‘Genericity of contracting elements in groups’, Preprint, 2017, arXiv:1707.06006.Google Scholar