Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T15:01:33.649Z Has data issue: false hasContentIssue false
  • English
  • Français

CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  22 June 2010

VOLKER RUNDE
VOLKER RUNDE*
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta, Canada T6G 2G1 (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, Daws introduced a notion of co-representation of abelian Hopf–von Neumann algebras on general reflexive Banach spaces. In this note, we show that this notion cannot be extended beyond subhomogeneous Hopf–von Neumann algebras. The key is our observation that, for a von Neumann algebra 𝔐 and a reflexive operator space E, the normal spatial tensor product 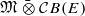is a Banach algebra if and only if 𝔐 is subhomogeneous or E is completely isomorphic to column Hilbert space.

Keywords

Hopf–von Neumann algebraco-representationreflexive operator spaceoperator algebracolumn Hilbert space

MSC classification

Secondary: 47L30: Abstract operator algebras on Hilbert spaces 46L99: None of the above, but in this section 47L25: Operator spaces (= matricially normed spaces)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 82 , Issue 2 , October 2010 , pp. 205 - 210
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Blecher, D. P., ‘A completely bounded characterization of operator algebras’, Math. Ann. 303 (1995), 227–239.CrossRefGoogle Scholar
[2]Blecher, D. P. and Le Merdy, C., Operator Algebras and their Modules. An Operator Space Approach, London Mathematical Society Monographs (New Series), 30 (Clarendon Press, Oxford, 2004).CrossRefGoogle Scholar
[3]Burckel, R. B., Weakly Almost Periodic Functions on Semigroups (Gordon and Breach Science Publishers, New York, 1970).Google Scholar
[4]Daws, M., ‘Weakly almost periodic functionals on the measure algebra’, Math. Z. 265 (2010), 61–78.CrossRefGoogle Scholar
[5]Effros, E. G. and Ruan, Z.-J., Operator Spaces, London Mathematical Society Monographs (New Series), 23 (Clarendon Press, Oxford, 2000).Google Scholar
[6]Eymard, P., ‘L’algèbre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
[7]Grothendieck, A., ‘Critères de compacité dans les espaces fonctionnels généraux’, Amer. J. Math. 74 (1953), 168–186.CrossRefGoogle Scholar
[8]Kraus, J., ‘The slice map problem for σ-weakly closed subspaces of von Neumann algebras’, Trans. Amer. Math. Soc. 279 (1983), 357–376.Google Scholar
[9]Pisier, G., ‘Non-commutative vector valued L p-spaces and completely p-summing maps’, Astérisque 247 (1998).Google Scholar