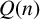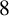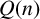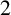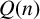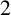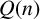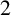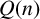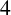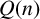1 Introduction
A partition
![]() $\pi $
of a positive integer n is a finite weakly decreasing sequence of positive integers
$\pi $
of a positive integer n is a finite weakly decreasing sequence of positive integers
![]() $\pi _1\geq \pi _2\geq \cdots \geq \pi _r$
such that
$\pi _1\geq \pi _2\geq \cdots \geq \pi _r$
such that
![]() $\sum _{i=1}^r\pi _i=n$
. The
$\sum _{i=1}^r\pi _i=n$
. The
![]() $\pi _i$
are called the parts of the partition
$\pi _i$
are called the parts of the partition
![]() $\pi $
. Let
$\pi $
. Let
![]() $p(n)$
denote the number of partitions of n with the convention that
$p(n)$
denote the number of partitions of n with the convention that
![]() $p(0)=1$
. The generating function of
$p(0)=1$
. The generating function of
![]() $p(n)$
, derived by Euler, is given by
$p(n)$
, derived by Euler, is given by
 $$ \begin{align*} \sum_{n=0}^{\infty} p(n)q^n=\dfrac{1}{(q;q)_{\infty}}, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty} p(n)q^n=\dfrac{1}{(q;q)_{\infty}}, \end{align*} $$
where, here and throughout this paper, we always assume that q is a complex number such that
![]() $|q|<1$
and adopt the customary notation:
$|q|<1$
and adopt the customary notation:
 $$ \begin{align*} (a;q)_{\infty}=\prod_{j=0}^{\infty}(1-aq^j). \end{align*} $$
$$ \begin{align*} (a;q)_{\infty}=\prod_{j=0}^{\infty}(1-aq^j). \end{align*} $$
In 1919, Ramanujan discovered three celebrated congruences for the partition function
![]() $p(n)$
(see [Reference Berndt and Ono4]), which were later confirmed by Atkin [Reference Atkin2] and Watson [Reference Watson15]: for any
$p(n)$
(see [Reference Berndt and Ono4]), which were later confirmed by Atkin [Reference Atkin2] and Watson [Reference Watson15]: for any
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\alpha \geq 1$
,
$\alpha \geq 1$
,
where
![]() $\delta _{p,\alpha }$
is the least positive integer satisfying
$\delta _{p,\alpha }$
is the least positive integer satisfying
![]() $24\delta _{p,\alpha }\equiv 1\pmod {p^{\alpha }}$
with
$24\delta _{p,\alpha }\equiv 1\pmod {p^{\alpha }}$
with
![]() ${p\in \{5,7,11\}}$
. Since then, congruence properties for various partition functions have been a hot topic in the theory of partitions and have motivated a large amount of research.
${p\in \{5,7,11\}}$
. Since then, congruence properties for various partition functions have been a hot topic in the theory of partitions and have motivated a large amount of research.
Another ingredient of the theory of partitions is the study of partition identities. In 1748, Euler [Reference Euler7] proved the most well-known partition theorem which states that there are as many partitions of n into distinct parts as into odd parts. In terms of the generating function,
 $$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=(-q;q)_{\infty}=\dfrac{1}{(q;q^2)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=(-q;q)_{\infty}=\dfrac{1}{(q;q^2)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}, \end{align} $$
where
![]() $Q(n)$
denotes the number of partitions of n into distinct parts. According to Euler’s pentagonal number theorem [Reference Andrews and Berndt1, page 17, (1.4.11)],
$Q(n)$
denotes the number of partitions of n into distinct parts. According to Euler’s pentagonal number theorem [Reference Andrews and Berndt1, page 17, (1.4.11)],
 $$ \begin{align*} (q;q)_{\infty}=\sum_{n=-\infty}^{\infty}(-1)^nq^{n(3n-1)/2}, \end{align*} $$
$$ \begin{align*} (q;q)_{\infty}=\sum_{n=-\infty}^{\infty}(-1)^nq^{n(3n-1)/2}, \end{align*} $$
we find that almost all values of
![]() $Q(n)$
are even, that is,
$Q(n)$
are even, that is,
Indeed,
![]() $Q(n)$
is odd if and only if n is a generalised pentagonal number. Motivated by (1.1)–(1.5), many scholars subsequently investigated congruence properties and arithmetic density properties of
$Q(n)$
is odd if and only if n is a generalised pentagonal number. Motivated by (1.1)–(1.5), many scholars subsequently investigated congruence properties and arithmetic density properties of
![]() $Q(n)$
. For instance, in 1997, Gordon and Ono [Reference Gordon and Ono8] proved the striking result that for any positive integer m,
$Q(n)$
. For instance, in 1997, Gordon and Ono [Reference Gordon and Ono8] proved the striking result that for any positive integer m,
![]() $Q(n)$
is divisible by
$Q(n)$
is divisible by
![]() $2^m$
for almost all nonnegative integers n, that is,
$2^m$
for almost all nonnegative integers n, that is,
The identity (1.6) is a powerful result on the arithmetic properties of
![]() $Q(n)$
. However, it is not a constructive result and the theory of modular forms used in the proof of (1.6) cannot be applied to derive the explicit congruences enjoyed by
$Q(n)$
. However, it is not a constructive result and the theory of modular forms used in the proof of (1.6) cannot be applied to derive the explicit congruences enjoyed by
![]() $Q(n)$
. Therefore, it is still of interest to find explicit congruences for
$Q(n)$
. Therefore, it is still of interest to find explicit congruences for
![]() $Q(n)$
.
$Q(n)$
.
In a recent paper, Merca [Reference Merca9] derived some congruences modulo
![]() $4$
and
$4$
and
![]() $8$
for
$8$
for
![]() $Q(n)$
by using Smoot’s Mathematica implementation [Reference Smoot13] of Radu’s algorithm [Reference Radu12] on Ramanujan–Kolberg identities for partition functions. At the end of his paper, Merca posed the following conjecture on congruences modulo powers of 2 for
$Q(n)$
by using Smoot’s Mathematica implementation [Reference Smoot13] of Radu’s algorithm [Reference Radu12] on Ramanujan–Kolberg identities for partition functions. At the end of his paper, Merca posed the following conjecture on congruences modulo powers of 2 for
![]() $Q(n)$
.
$Q(n)$
.
Conjecture 1.1 (Merca [Reference Merca9], Conjecture).
Let
![]() $(p,k)\in S$
. For any
$(p,k)\in S$
. For any
![]() $n\not \equiv 0\pmod {p}$
,
$n\not \equiv 0\pmod {p}$
,
where
 $$ \begin{align} S\in\{ &(11,5),(13,6),(17,8),(19,9),(23,11),(31,3),(37,6),\nonumber\\ &(41,8),(43,9),(47,11),(59,6),(61,6),(67,10),(71,13),\nonumber\\ &(79,3),(83,5),(89,9),(103,3),(107,6),(109,6),(113,9)\}. \end{align} $$
$$ \begin{align} S\in\{ &(11,5),(13,6),(17,8),(19,9),(23,11),(31,3),(37,6),\nonumber\\ &(41,8),(43,9),(47,11),(59,6),(61,6),(67,10),(71,13),\nonumber\\ &(79,3),(83,5),(89,9),(103,3),(107,6),(109,6),(113,9)\}. \end{align} $$
In this paper, we prove the following result.
Theorem 1.2. Let S be defined as in (1.7). Then for any
![]() $(p,k)\in S$
,
$(p,k)\in S$
,
 $$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{2^k}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{2^k}, \end{align} $$
where
![]() $c_p$
is given in Table 1.
$c_p$
is given in Table 1.
Table 1 A table of values of
![]() $c_p$
.
$c_p$
.

As an immediate consequence of (1.8), we obtain the following congruences and internal congruences enjoyed by
![]() $Q(n)$
, which confirms Conjecture 1.1.
$Q(n)$
, which confirms Conjecture 1.1.
Corollary 1.3. Let S be defined as in (1.7). Then for any
![]() $(p,k)\in S$
and
$(p,k)\in S$
and
![]() $1\leq i\leq p-1$
,
$1\leq i\leq p-1$
,
Moreover, for any
![]() $n\geq 0$
,
$n\geq 0$
,
where
![]() $c_p$
is given in Table 1.
$c_p$
is given in Table 1.
The following theorem shows that there are an infinite family of congruence relations of the form (1.8) satisfied by
![]() $Q(n)$
.
$Q(n)$
.
Theorem 1.4. Let
![]() $p\geq 5$
be a prime number. If
$p\geq 5$
be a prime number. If
![]() $\big(\frac{-24}{p}\big)=-1$
, then
$\big(\frac{-24}{p}\big)=-1$
, then
 $$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align} $$
where
![]() $\big (\frac {\cdot }{p}\big )$
is the Legendre symbol and
$\big (\frac {\cdot }{p}\big )$
is the Legendre symbol and
 $$ \begin{align} (\pm p-1)/6= \begin{cases} (p-1)/6 &\textrm{if } p\equiv1\pmod{6},\\ (-p-1)/6 &\textrm{if } p\equiv5\pmod{6}. \end{cases} \end{align} $$
$$ \begin{align} (\pm p-1)/6= \begin{cases} (p-1)/6 &\textrm{if } p\equiv1\pmod{6},\\ (-p-1)/6 &\textrm{if } p\equiv5\pmod{6}. \end{cases} \end{align} $$
The rest of this paper is organised as follows. In Section 2, we collect some notation and terminology on modular forms. The proof of Theorem 1.2 is presented in Section 3 and that of Theorem 1.4 in Section 4. Finally, we pose a conjecture on congruence relations for
![]() $Q(n)$
modulo
$Q(n)$
modulo
![]() $4$
which strengthens both (1.9) and a result of Merca.
$4$
which strengthens both (1.9) and a result of Merca.
2 Preliminaries
We first recall some terminology from the theory of modular forms. The full modular group is given by
 $$ \begin{align*} \Gamma=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\colon a, b, c, d\in\mathbb{Z}, \text{ and } ad-bc=1\bigg\}, \end{align*} $$
$$ \begin{align*} \Gamma=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\colon a, b, c, d\in\mathbb{Z}, \text{ and } ad-bc=1\bigg\}, \end{align*} $$
and for a positive integer N, the congruence subgroup
![]() $\Gamma _0(N)$
is defined by
$\Gamma _0(N)$
is defined by
 $$ \begin{align*} \Gamma_0(N)=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\in\Gamma \colon c\equiv 0\pmod{N}\bigg\}. \end{align*} $$
$$ \begin{align*} \Gamma_0(N)=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\in\Gamma \colon c\equiv 0\pmod{N}\bigg\}. \end{align*} $$
Let
![]() $\gamma $
be the matrix
$\gamma $
be the matrix
![]() $(\begin {smallmatrix}a &b\\ c &d\end {smallmatrix})$
from now on. Then
$(\begin {smallmatrix}a &b\\ c &d\end {smallmatrix})$
from now on. Then
![]() $\gamma $
acts on
$\gamma $
acts on
![]() $\tau \in \mathbb {C}$
by the linear fractional transformation
$\tau \in \mathbb {C}$
by the linear fractional transformation
Let N, k be positive integers and
![]() $\mathbb {H}=\{\tau \in \mathbb {C}\colon \mathrm {Im}(\tau )>0\}$
. A holomorphic function
$\mathbb {H}=\{\tau \in \mathbb {C}\colon \mathrm {Im}(\tau )>0\}$
. A holomorphic function
![]() $f\colon \mathbb {H}\rightarrow \mathbb {C}$
is called a modular function of weight k for
$f\colon \mathbb {H}\rightarrow \mathbb {C}$
is called a modular function of weight k for
![]() $\Gamma _0(N)$
if it satisfies the following two conditions:
$\Gamma _0(N)$
if it satisfies the following two conditions:
-
(1) for all
 $\gamma \in \Gamma _0(N)$
,
$\gamma \in \Gamma _0(N)$
,
 $f(\gamma \tau )=(c\tau +d)^kf(\tau )$
;
$f(\gamma \tau )=(c\tau +d)^kf(\tau )$
; -
(2) for any
 $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
 $(c\tau +d)^{-k}f(\gamma \tau )$
has a Fourier expansion of the form
$(c\tau +d)^{-k}f(\gamma \tau )$
has a Fourier expansion of the form  $$ \begin{align*} (c\tau+d)^{-k}f(\gamma\tau)=\sum_{n=n_{\gamma}}^{\infty} a(n)q_{w_{\gamma}}^n, \end{align*} $$
$$ \begin{align*} (c\tau+d)^{-k}f(\gamma\tau)=\sum_{n=n_{\gamma}}^{\infty} a(n)q_{w_{\gamma}}^n, \end{align*} $$
where
 $a(n_{\gamma })\neq 0$
,
$a(n_{\gamma })\neq 0$
,
 $q_{w_{\gamma }}=e^{2\pi i\tau /w_{\gamma }}$
and
$q_{w_{\gamma }}=e^{2\pi i\tau /w_{\gamma }}$
and
 $w_{\gamma }={N}/{\gcd (c^2, N)}$
.
$w_{\gamma }={N}/{\gcd (c^2, N)}$
.
In particular, if
![]() $n_{\gamma } \geq 0$
for all
$n_{\gamma } \geq 0$
for all
![]() $\gamma \in \Gamma $
, then we call f a modular form of weight k for
$\gamma \in \Gamma $
, then we call f a modular form of weight k for
![]() $\Gamma _0(N)$
. A modular function with weight 0 for
$\Gamma _0(N)$
. A modular function with weight 0 for
![]() $\Gamma _0(N)$
is referred to as a modular function for
$\Gamma _0(N)$
is referred to as a modular function for
![]() $\Gamma _0(N)$
. For a modular function
$\Gamma _0(N)$
. For a modular function
![]() $f(\tau )$
of weight k with respect to
$f(\tau )$
of weight k with respect to
![]() $\Gamma _0(N)$
, the order of
$\Gamma _0(N)$
, the order of
![]() $f(\tau )$
at the cusp
$f(\tau )$
at the cusp
![]() $a/c\in \mathbb {Q}\cup \{\infty \}$
is defined by
$a/c\in \mathbb {Q}\cup \{\infty \}$
is defined by
for some
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $\gamma \infty =a/c$
;
$\gamma \infty =a/c$
;
![]() $\mathrm {ord}_{a/c}(f)$
is well defined (see [Reference Diamond and Shurman6, page 72]).
$\mathrm {ord}_{a/c}(f)$
is well defined (see [Reference Diamond and Shurman6, page 72]).
Radu [Reference Radu12] developed the Ramanujan–Kolberg algorithm to derive the Ramanujan– Kolberg identities on a class of partition functions defined in terms of eta-quotients using modular functions for
![]() $\Gamma _0(N)$
(see [Reference Paule, Radu, Beveridge, Griggs, Hogben, Musiker and Tetali11]). Smoot [Reference Smoot13] developed a Mathematica package
$\Gamma _0(N)$
(see [Reference Paule, Radu, Beveridge, Griggs, Hogben, Musiker and Tetali11]). Smoot [Reference Smoot13] developed a Mathematica package
![]() $\mathtt {RaduRK}$
to implement Radu’s algorithm.
$\mathtt {RaduRK}$
to implement Radu’s algorithm.
Let the partition function
![]() $a(n)$
be defined by
$a(n)$
be defined by
 $$ \begin{align} \sum_{n=0}^{\infty} a(n)q^n=\prod_{\delta|M} (q^{\delta}, q^{\delta})_{\infty}^{r_{\delta}}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} a(n)q^n=\prod_{\delta|M} (q^{\delta}, q^{\delta})_{\infty}^{r_{\delta}}, \end{align} $$
where M,
![]() $\delta $
are positive integers and
$\delta $
are positive integers and
![]() $r_{\delta }$
are integers. For any
$r_{\delta }$
are integers. For any
![]() $m\geq 1$
and
$m\geq 1$
and
![]() $0\leq t\leq m-1$
, Radu [Reference Radu12] defined
$0\leq t\leq m-1$
, Radu [Reference Radu12] defined
 $$ \begin{align*} g_{m,t}(\tau) = q^{{(t+\ell)}/{m}}\sum\limits_{n=0}^{\infty} a(mn+t)q^n, \end{align*} $$
$$ \begin{align*} g_{m,t}(\tau) = q^{{(t+\ell)}/{m}}\sum\limits_{n=0}^{\infty} a(mn+t)q^n, \end{align*} $$
where
 $$ \begin{align*} \ell=\frac{1}{24}\sum\limits_{\delta|M}\delta r_{\delta}, \end{align*} $$
$$ \begin{align*} \ell=\frac{1}{24}\sum\limits_{\delta|M}\delta r_{\delta}, \end{align*} $$
and gave a criterion for a function involving
![]() $g_{m,t}(\tau )$
to be a modular function with respect to
$g_{m,t}(\tau )$
to be a modular function with respect to
![]() $\Gamma _0(N)$
, where N satisfies the following conditions, with
$\Gamma _0(N)$
, where N satisfies the following conditions, with
![]() $\kappa =\gcd (1-m^2, 24)$
:
$\kappa =\gcd (1-m^2, 24)$
:
-
(1) for every prime p,
 $p \mid m$
implies
$p \mid m$
implies
 $p \mid N$
;
$p \mid N$
; -
(2) for every
 $\delta $
dividing M with
$\delta $
dividing M with
 $r_{\delta }\neq 0$
,
$r_{\delta }\neq 0$
,
 $\delta \mid M$
implies
$\delta \mid M$
implies
 $\delta \mid mN$
;
$\delta \mid mN$
; -
(3)
 $\kappa mN^2\sum _{\delta |M}{r_{\delta }}/{\delta }\equiv 0\pmod {24}$
;
$\kappa mN^2\sum _{\delta |M}{r_{\delta }}/{\delta }\equiv 0\pmod {24}$
; -
(4)
 $\kappa N \sum _{\delta |M} r_{\delta } \equiv 0\pmod {8}$
;
$\kappa N \sum _{\delta |M} r_{\delta } \equiv 0\pmod {8}$
; -
(5)
 ${24 m}/{\gcd (\kappa (-24 t-\sum _{\delta |M}\delta r_{\delta }), 24 m)} \mid N ;$
${24 m}/{\gcd (\kappa (-24 t-\sum _{\delta |M}\delta r_{\delta }), 24 m)} \mid N ;$
-
(6) if
 $2 \mid m$
, then
$2 \mid m$
, then
 $\kappa N\equiv 0\pmod {4}$
and
$\kappa N\equiv 0\pmod {4}$
and
 $8 \mid Ns$
, or
$8 \mid Ns$
, or
 $2 \mid s$
and
$2 \mid s$
and
 $8 \mid N(1-j)$
, where
$8 \mid N(1-j)$
, where
 $\prod _{\delta |M} \delta ^{|r_{\delta }|}=2^sj$
and
$\prod _{\delta |M} \delta ^{|r_{\delta }|}=2^sj$
and
 $j, s\in \mathbb {Z}$
with j odd.
$j, s\in \mathbb {Z}$
with j odd.
Given a positive integer n and an integer x, we denote by
![]() $[x]_n$
the residue class of x modulo n. Let
$[x]_n$
the residue class of x modulo n. Let
Define the set
 $$ \begin{align*} P_m(t)=\bigg\{\bigg[ts+\frac{s-1}{24}\sum_{\delta|M}\delta r_{\delta}\bigg]_m : s\in\mathbb{S}_{24m}\bigg\}. \end{align*} $$
$$ \begin{align*} P_m(t)=\bigg\{\bigg[ts+\frac{s-1}{24}\sum_{\delta|M}\delta r_{\delta}\bigg]_m : s\in\mathbb{S}_{24m}\bigg\}. \end{align*} $$
Recall that the Dedekind eta-function
![]() $\eta (\tau )$
is defined by
$\eta (\tau )$
is defined by
 $$ \begin{align*} \eta(\tau)=q^{{1}/{24}}\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
$$ \begin{align*} \eta(\tau)=q^{{1}/{24}}\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
where
![]() $q=e^{2\pi i \tau }$
and
$q=e^{2\pi i \tau }$
and
![]() $\tau \in \mathbb {H}$
.
$\tau \in \mathbb {H}$
.
Theorem 2.1 [Reference Radu12, Theorem 45].
For a partition function
![]() $a(n)$
defined as in (2.1), and integers
$a(n)$
defined as in (2.1), and integers
![]() $m\geq 1, 0\leq t\leq m-1$
, suppose that N is a positive integer satisfying the conditions (1)–(6). Let
$m\geq 1, 0\leq t\leq m-1$
, suppose that N is a positive integer satisfying the conditions (1)–(6). Let
 $$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau), \end{align*} $$
$$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau), \end{align*} $$
where
![]() $s_{\delta }$
are integers. Then
$s_{\delta }$
are integers. Then
![]() $F(\tau )$
is a modular function for
$F(\tau )$
is a modular function for
![]() $\Gamma _0(N)$
if and only if the
$\Gamma _0(N)$
if and only if the
![]() $s_{\delta }$
satisfy the following conditions:
$s_{\delta }$
satisfy the following conditions:
-
(1)
 $|P_m(t)| \sum _{\delta |M}r_{\delta }+\sum _{\delta |N} s_{\delta } =0;$
$|P_m(t)| \sum _{\delta |M}r_{\delta }+\sum _{\delta |N} s_{\delta } =0;$
-
(2)
 $\sum _{t'\in P_m(t)}{(1-m^2)(24t'+\sum _{\delta |M}\delta r_{\delta })}/{m} +|P_m(t)|m\sum _{\delta |M}\delta r_{\delta }+\sum _{\delta |N}\delta s_{\delta }\equiv 0\pmod {24};$
$\sum _{t'\in P_m(t)}{(1-m^2)(24t'+\sum _{\delta |M}\delta r_{\delta })}/{m} +|P_m(t)|m\sum _{\delta |M}\delta r_{\delta }+\sum _{\delta |N}\delta s_{\delta }\equiv 0\pmod {24};$
-
(3)
 $|P_m(t)|mN\sum _{\delta |M}{r_{\delta }}/{\delta }+\sum _{\delta |N} ({N}/{\delta })s_{\delta } \equiv 0\pmod {24};$
$|P_m(t)|mN\sum _{\delta |M}{r_{\delta }}/{\delta }+\sum _{\delta |N} ({N}/{\delta })s_{\delta } \equiv 0\pmod {24};$
-
(4)
 ${(\prod _{\delta |M}(m\delta )^{|r_{\delta }|})}^{|P_{m}(t)|}\prod _{\delta |N}\delta ^{|s_{\delta }|}$
is a square.
${(\prod _{\delta |M}(m\delta )^{|r_{\delta }|})}^{|P_{m}(t)|}\prod _{\delta |N}\delta ^{|s_{\delta }|}$
is a square.
Radu [Reference Radu12, Theorem 47] also gave lower bounds for the orders of
![]() $F(\tau )$
at cusps of
$F(\tau )$
at cusps of
![]() $\Gamma _0(N)$
.
$\Gamma _0(N)$
.
Theorem 2.2. For a partition function
![]() $a(n)$
defined as in (2.1) and integers
$a(n)$
defined as in (2.1) and integers
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $0\leq t\leq m-1$
, let
$0\leq t\leq m-1$
, let
 $$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau) \end{align*} $$
$$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau) \end{align*} $$
be a modular function for
![]() $\Gamma _0(N)$
, where
$\Gamma _0(N)$
, where
![]() $s_{\delta }$
are integers and N satisfies the conditions (1)–(6). Let
$s_{\delta }$
are integers and N satisfies the conditions (1)–(6). Let
![]() $\{s_1, s_2,\ldots ,s_{\epsilon }\}$
be a complete set of inequivalent cusps of
$\{s_1, s_2,\ldots ,s_{\epsilon }\}$
be a complete set of inequivalent cusps of
![]() $\Gamma _0(N)$
and, for
$\Gamma _0(N)$
and, for
![]() $1\leq i \leq \epsilon $
, let
$1\leq i \leq \epsilon $
, let
![]() $\gamma _i\in \Gamma $
be such that
$\gamma _i\in \Gamma $
be such that
![]() $\gamma _i\infty = s_i$
. Then
$\gamma _i\infty = s_i$
. Then
 $$ \begin{align*} \mathrm{ord}_{s_i}(F(\tau)) \geq \frac{N}{\gcd(c^2, N)}(|P_m(t)|p(\gamma_i)+p^*(\gamma_i)), \end{align*} $$
$$ \begin{align*} \mathrm{ord}_{s_i}(F(\tau)) \geq \frac{N}{\gcd(c^2, N)}(|P_m(t)|p(\gamma_i)+p^*(\gamma_i)), \end{align*} $$
where
 $$ \begin{align*} p(\gamma_i)=\min_{\lambda\in\{0, 1, \ldots, m-1\}}\frac{1}{24}\sum_{\delta|M} r_{\delta}\frac{\gcd^2(\delta(a+\kappa\lambda c), mc)}{\delta m} \end{align*} $$
$$ \begin{align*} p(\gamma_i)=\min_{\lambda\in\{0, 1, \ldots, m-1\}}\frac{1}{24}\sum_{\delta|M} r_{\delta}\frac{\gcd^2(\delta(a+\kappa\lambda c), mc)}{\delta m} \end{align*} $$
and
 $$ \begin{align*} p^*(\gamma_i)=\frac{1}{24}\sum_{\delta|N}s_{\delta}\frac{\gcd^2(\delta, c)}{\delta}. \end{align*} $$
$$ \begin{align*} p^*(\gamma_i)=\frac{1}{24}\sum_{\delta|N}s_{\delta}\frac{\gcd^2(\delta, c)}{\delta}. \end{align*} $$
The following theorem of Sturm [Reference Sturm14, Theorem 1] plays an important role in proving congruences using the theory of modular forms.
Theorem 2.3. Let k be an integer and
![]() $g(\tau )=\sum _{n=0}^{\infty } c(n)q^n$
a modular form of weight k for
$g(\tau )=\sum _{n=0}^{\infty } c(n)q^n$
a modular form of weight k for
![]() $\Gamma _0(N)$
. For any given positive integer u, if
$\Gamma _0(N)$
. For any given positive integer u, if
![]() $c(n)\equiv 0\pmod {u}$
holds for all
$c(n)\equiv 0\pmod {u}$
holds for all
![]() $n\leq ({kN}/{12})\prod _{p|N, \, p\mathrm {~prime}}{(1+{1}/{p})}$
, then
$n\leq ({kN}/{12})\prod _{p|N, \, p\mathrm {~prime}}{(1+{1}/{p})}$
, then
![]() $c(n)\equiv 0\pmod {u}$
holds for any
$c(n)\equiv 0\pmod {u}$
holds for any
![]() $n\geq 0$
.
$n\geq 0$
.
3 Proof of Theorem 1.2
This section is devoted to the proof of Theorem 1.2. The following lemma plays a vital role in the proof of Theorem 1.2.
Lemma 3.1. Let
![]() $p$
be a prime with
$p$
be a prime with
![]() $p\ge5$
and define
$p\ge5$
and define
![]() $k_1 = \lceil(p^2-1)/48p\rceil$
and
$k_1 = \lceil(p^2-1)/48p\rceil$
and
![]() ${k_2 = \lceil(p^2-1)/48p^2\rceil}$
. Then for any constant c,
${k_2 = \lceil(p^2-1)/48p^2\rceil}$
. Then for any constant c,
 $$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)}\sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c\bigg)} \end{align*} $$
$$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)}\sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c\bigg)} \end{align*} $$
is a modular form of weight
![]() $12k_1+4k_2$
for
$12k_1+4k_2$
for
![]() $\Gamma _0(2p)$
.
$\Gamma _0(2p)$
.
Proof. Recall that the generating function of
![]() $Q(n)$
is
$Q(n)$
is
 $$ \begin{align*} \sum_{n=0}^{\infty} Q(n)q^n=\frac{(q^2; q^2)_{\infty}}{(q; q)_{\infty}}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty} Q(n)q^n=\frac{(q^2; q^2)_{\infty}}{(q; q)_{\infty}}. \end{align*} $$
Taking
![]() $M=2$
,
$M=2$
,
![]() $(r_1, r_2)=(-1,1)$
,
$(r_1, r_2)=(-1,1)$
,
![]() $m=p$
,
$m=p$
,
![]() $t=(p^2-1)/24$
in Theorem 2.1, one can find that
$t=(p^2-1)/24$
in Theorem 2.1, one can find that
![]() $N=2p$
satisfies the conditions (1)–(6), and for
$N=2p$
satisfies the conditions (1)–(6), and for
![]() $(s_1, s_2, s_p, s_{2p})=(0,0,1, -1)$
,
$(s_1, s_2, s_p, s_{2p})=(0,0,1, -1)$
,
 $$ \begin{align*} F(\tau)=q^{{p}/{24}}\frac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n \end{align*} $$
$$ \begin{align*} F(\tau)=q^{{p}/{24}}\frac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n \end{align*} $$
is a modular function for
![]() $\Gamma _0(2p)$
.
$\Gamma _0(2p)$
.
By Theorem 2.2, we derive lower bounds for the orders of
![]() $F(\tau )$
at the cusps of
$F(\tau )$
at the cusps of
![]() $\Gamma _0(2p)$
:
$\Gamma _0(2p)$
:
 $$ \begin{align*} \mathrm{ord}_0(F(\tau)) \geq-\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau))\geq -\frac{1}{24p},\\ \mathrm{ord}_{1/p}(F(\tau)) \geq \frac{2p^2-1}{24p}, &\quad \mathrm{ord}_{\infty}(F(\tau))\geq -\frac{p^2-1}{24p}, \end{align*} $$
$$ \begin{align*} \mathrm{ord}_0(F(\tau)) \geq-\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau))\geq -\frac{1}{24p},\\ \mathrm{ord}_{1/p}(F(\tau)) \geq \frac{2p^2-1}{24p}, &\quad \mathrm{ord}_{\infty}(F(\tau))\geq -\frac{p^2-1}{24p}, \end{align*} $$
which implies that
 $$ \begin{align*} \mathrm{ord}_0(F(\tau)-c) \geq -\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau)-c) \geq 0,\\ \mathrm{ord}_{1/p}(F(\tau)-c) \geq 0, &\quad \mathrm{ord}_{\infty}(F(\tau)-c) \geq -\frac{p^2-1}{24p}. \end{align*} $$
$$ \begin{align*} \mathrm{ord}_0(F(\tau)-c) \geq -\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau)-c) \geq 0,\\ \mathrm{ord}_{1/p}(F(\tau)-c) \geq 0, &\quad \mathrm{ord}_{\infty}(F(\tau)-c) \geq -\frac{p^2-1}{24p}. \end{align*} $$
By [Reference Ono10, Theorems 1.64 and 1.65], one easily shows
 $$ \begin{align*} F_1(\tau)=\eta^{24}(\tau) \quad \text{and} \quad F_2(\tau)=\frac{\eta^{16}(2p\tau)}{\eta^8(p\tau)} \end{align*} $$
$$ \begin{align*} F_1(\tau)=\eta^{24}(\tau) \quad \text{and} \quad F_2(\tau)=\frac{\eta^{16}(2p\tau)}{\eta^8(p\tau)} \end{align*} $$
are modular forms with weight 12 and 4 for
![]() $\Gamma _0(2p)$
, respectively, and the orders at the cusps of
$\Gamma _0(2p)$
, respectively, and the orders at the cusps of
![]() $\Gamma _0(2p)$
are
$\Gamma _0(2p)$
are
 $$ \begin{align*} \mathrm{ord}_0(F_1(\tau)) =2p, \quad \mathrm{ord}_{1/2}(F_1(\tau)) =p, &\quad \mathrm{ord}_{1/p}(F_1(\tau)) =2, \quad \mathrm{ord}_{\infty}(F_1(\tau)) =1,\\ \mathrm{ord}_0(F_2(\tau)) =0, \quad \mathrm{ord}_{1/2}(F_2(\tau)) =1, &\quad \mathrm{ord}_{1/p}(F_2(\tau)) =0, \quad \mathrm{ord}_{\infty}(F_2(\tau)) =p. \end{align*} $$
$$ \begin{align*} \mathrm{ord}_0(F_1(\tau)) =2p, \quad \mathrm{ord}_{1/2}(F_1(\tau)) =p, &\quad \mathrm{ord}_{1/p}(F_1(\tau)) =2, \quad \mathrm{ord}_{\infty}(F_1(\tau)) =1,\\ \mathrm{ord}_0(F_2(\tau)) =0, \quad \mathrm{ord}_{1/2}(F_2(\tau)) =1, &\quad \mathrm{ord}_{1/p}(F_2(\tau)) =0, \quad \mathrm{ord}_{\infty}(F_2(\tau)) =p. \end{align*} $$
Therefore, the orders of
![]() $F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$
at all cusps of
$F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$
at all cusps of
![]() $\Gamma _0(2p)$
are nonnegative, and so
$\Gamma _0(2p)$
are nonnegative, and so
![]() $F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$
is a modular form with weight
$F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$
is a modular form with weight
![]() $12k_2+4k_2$
for
$12k_2+4k_2$
for
![]() $\Gamma _0(2p)$
. This completes the proof.
$\Gamma _0(2p)$
. This completes the proof.
Proof of Theorem 1.2.
Fix
![]() $k\ge 1$
. By Lemma 3.1 and Sturm’s theorem, to prove
$k\ge 1$
. By Lemma 3.1 and Sturm’s theorem, to prove
 $$ \begin{align*} \dfrac{(q^p;q^p)_{\infty}}{(q^{2p};q^{2p})_{\infty}} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\equiv 0\pmod{2^k}, \end{align*} $$
$$ \begin{align*} \dfrac{(q^p;q^p)_{\infty}}{(q^{2p};q^{2p})_{\infty}} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\equiv 0\pmod{2^k}, \end{align*} $$
we only need to check that the coefficients of the first
![]() $l_p=(p+1)(3k_1+k_2)$
terms of the expansion of
$l_p=(p+1)(3k_1+k_2)$
terms of the expansion of
 $$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\bigg)} \end{align*} $$
$$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\bigg)} \end{align*} $$
are congruent to 0 modulo
![]() $2^k$
. Here,
$2^k$
. Here,
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are defined in Lemma 3.1 and the corresponding
$k_2$
are defined in Lemma 3.1 and the corresponding
![]() $l_p$
are displayed in Table 2. This information allows us to do the computations to complete the proof of Theorem 1.2.
$l_p$
are displayed in Table 2. This information allows us to do the computations to complete the proof of Theorem 1.2.
Table 2 A table of values of
![]() $l_p$
.
$l_p$
.

4 Proof of Theorem 1.4
In this section, we give a proof of Theorem 1.4. Before starting the proof, we need to introduce Ramanujan’s theta function, given by
 $$ \begin{align} f(a,b)=\sum_{n=0}^{\infty} a^{n(n+1)/2}b^{n(n-1)/2}=(-a,-b,ab;ab)_{\infty},\quad|ab|<1, \end{align} $$
$$ \begin{align} f(a,b)=\sum_{n=0}^{\infty} a^{n(n+1)/2}b^{n(n-1)/2}=(-a,-b,ab;ab)_{\infty},\quad|ab|<1, \end{align} $$
where the last identity in (4.1) is the celebrated Jacobi triple product [Reference Andrews and Berndt1, page 17, (1.4.8)]. Two important cases of
![]() $f(a,b)$
are
$f(a,b)$
are
 $$ \begin{align} \varphi(q) &:=f(q,q)=\sum_{n=0}^{\infty} q^{n^2}=\dfrac{(q^2;q^2)_{\infty}^5}{(q;q)_{\infty}^2(q^4;q^4)_{\infty}^2},\\ f(-q) &:=f(-q,-q^2)=\sum_{n=-\infty}^{\infty} q^{n(3n+1)/2}=(q;q)_{\infty}.\nonumber \end{align} $$
$$ \begin{align} \varphi(q) &:=f(q,q)=\sum_{n=0}^{\infty} q^{n^2}=\dfrac{(q^2;q^2)_{\infty}^5}{(q;q)_{\infty}^2(q^4;q^4)_{\infty}^2},\\ f(-q) &:=f(-q,-q^2)=\sum_{n=-\infty}^{\infty} q^{n(3n+1)/2}=(q;q)_{\infty}.\nonumber \end{align} $$
Replacing q by
![]() $-q$
in (4.2) yields
$-q$
in (4.2) yields
 $$ \begin{align*} \varphi(-q)=\dfrac{(q;q)_{\infty}^2}{(q^2;q^2)_{\infty}}. \end{align*} $$
$$ \begin{align*} \varphi(-q)=\dfrac{(q;q)_{\infty}^2}{(q^2;q^2)_{\infty}}. \end{align*} $$
The following p-dissections for
![]() $\varphi (-q)$
and
$\varphi (-q)$
and
![]() $f(-q)$
play an important role in the proof of Theorem 1.4.
$f(-q)$
play an important role in the proof of Theorem 1.4.
Lemma 4.1. Let
![]() $p\geq 5$
be a prime number. Then
$p\geq 5$
be a prime number. Then
 $$ \begin{align} \varphi(-q) &=\varphi({-}q^{p^2})+2\sum_{j=1}^{(p-1)/2}q^{{\kern1.2pt}j^2} f({-}q^{p^2+2pj},-q^{p^2-2pj}), \end{align} $$
$$ \begin{align} \varphi(-q) &=\varphi({-}q^{p^2})+2\sum_{j=1}^{(p-1)/2}q^{{\kern1.2pt}j^2} f({-}q^{p^2+2pj},-q^{p^2-2pj}), \end{align} $$
 $$ \begin{align} f(-q) &=\sum_{\substack{k=-(p-1)/2\\ k\neq(\pm p-1)/6}}^{(p-1)/2}(-1)^kq^{k(3k+1)/2} f({-}q^{(3p^2+(6k+1)p)/2},-q^{(3p^2-(6k+1)p)/2})\nonumber\\ &\quad+(-1)^{(\pm p-1)/6}q^{(p^2-1)/24}f({-}q^{p^2}), \end{align} $$
$$ \begin{align} f(-q) &=\sum_{\substack{k=-(p-1)/2\\ k\neq(\pm p-1)/6}}^{(p-1)/2}(-1)^kq^{k(3k+1)/2} f({-}q^{(3p^2+(6k+1)p)/2},-q^{(3p^2-(6k+1)p)/2})\nonumber\\ &\quad+(-1)^{(\pm p-1)/6}q^{(p^2-1)/24}f({-}q^{p^2}), \end{align} $$
where
![]() $(\pm p-1)/6$
is defined as in (1.10). Further, for
$(\pm p-1)/6$
is defined as in (1.10). Further, for
![]() $-(p-1)/2\leq k\leq (p-1)/2$
and
$-(p-1)/2\leq k\leq (p-1)/2$
and
![]() $k\neq (\pm p-1)/6$
,
$k\neq (\pm p-1)/6$
,
Proof. The identity (4.3) follows immediately from [Reference Berndt3, page 49]. The identity (4.4) appears in [Reference Cui and Gu5, Theorem 2.2].
Proof of Theorem 1.4.
From (1.4), we find that
 $$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}^2}{(q;q)_{\infty}^4}\cdot \dfrac{(q;q)_{\infty}^3}{(q^2;q^2)_{\infty}}\equiv\varphi(-q)\cdot f(-q)\pmod{4}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}^2}{(q;q)_{\infty}^4}\cdot \dfrac{(q;q)_{\infty}^3}{(q^2;q^2)_{\infty}}\equiv\varphi(-q)\cdot f(-q)\pmod{4}. \end{align} $$
For a prime
![]() $p\geq 5$
,
$p\geq 5$
,
![]() $0\leq j\leq (p-1)/2$
,
$0\leq j\leq (p-1)/2$
,
![]() $-(p-1)/2\leq k\leq (p-1)/2$
, assume that
$-(p-1)/2\leq k\leq (p-1)/2$
, assume that
which implies that
Since
![]() $\big(\frac{-24}{p}\big)=-1$
, we get
$\big(\frac{-24}{p}\big)=-1$
, we get
![]() $j=0$
and
$j=0$
and
![]() $k=(\pm p-1)/6$
. Substituting (4.3) and (4.4) into (4.5), we find that
$k=(\pm p-1)/6$
. Substituting (4.3) and (4.4) into (4.5), we find that
 $$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n &\equiv(-1)^{(\pm p-1)/6}\varphi({-}q^p)f({-}q^p)\nonumber\\ &\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n &\equiv(-1)^{(\pm p-1)/6}\varphi({-}q^p)f({-}q^p)\nonumber\\ &\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$
where we have used (4.5) in the last congruence. The congruence (1.9) follows. This completes the proof of Theorem 1.4.
5 Concluding remarks
One can use Lemma 3.1 to establish congruence relations satisfied by
![]() $Q(n)$
similar to (1.8) for other primes p. For example,
$Q(n)$
similar to (1.8) for other primes p. For example,
 $$ \begin{align*} \sum_{n=0}^{\infty} Q(127n+672)q^n &\equiv\sum_{n=0}^{\infty} Q(n)q^{127n}\pmod{2^3},\\ \sum_{n=0}^{\infty} Q(131n+715)q^n &\equiv43\sum_{n=0}^{\infty} Q(n)q^{131n}\pmod{2^7},\\ \sum_{n=0}^{\infty} Q(137n+782)q^n &\equiv71\sum_{n=0}^{\infty} Q(n)q^{137n}\pmod{2^8},\\ \sum_{n=0}^{\infty} Q(139n+805)q^n &\equiv803\sum_{n=0}^{\infty} Q(n)q^{139n}\pmod{2^{10}}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty} Q(127n+672)q^n &\equiv\sum_{n=0}^{\infty} Q(n)q^{127n}\pmod{2^3},\\ \sum_{n=0}^{\infty} Q(131n+715)q^n &\equiv43\sum_{n=0}^{\infty} Q(n)q^{131n}\pmod{2^7},\\ \sum_{n=0}^{\infty} Q(137n+782)q^n &\equiv71\sum_{n=0}^{\infty} Q(n)q^{137n}\pmod{2^8},\\ \sum_{n=0}^{\infty} Q(139n+805)q^n &\equiv803\sum_{n=0}^{\infty} Q(n)q^{139n}\pmod{2^{10}}. \end{align*} $$
However, the corresponding bound
![]() $l_p$
will become much larger as p increases.
$l_p$
will become much larger as p increases.
Merca [Reference Merca9] proved the following infinite family of congruences modulo
![]() $4$
for
$4$
for
![]() $Q(n)$
.
$Q(n)$
.
Theorem 5.1. Let
![]() $p\geq 5$
be a prime number such that
$p\geq 5$
be a prime number such that
![]() $p\not \equiv 1\pmod {24}$
. Then for any
$p\not \equiv 1\pmod {24}$
. Then for any
![]() $n\not \equiv 0\pmod {p}$
,
$n\not \equiv 0\pmod {p}$
,
The congruence (1.8) together with numerical evidence suggests the following conjecture, which contains (1.9) and (5.1) as special cases.
Conjecture 5.2. Let
![]() $p\geq 5$
be a prime number such that
$p\geq 5$
be a prime number such that
![]() $p\not \equiv 1\pmod {24}$
. Then
$p\not \equiv 1\pmod {24}$
. Then
 $$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$
where
![]() $c_p=-1$
or
$c_p=-1$
or
![]() $1$
.
$1$
.