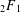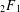Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Ji-Cai
2017.
Proof of some divisibility results on sums involving binomial coefficients.
Journal of Number Theory,
Vol. 180,
Issue. ,
p.
566.
Liu, Ji-Cai
2018.
Some supercongruences on truncated hypergeometric series.
Journal of Difference Equations and Applications,
Vol. 24,
Issue. 3,
p.
438.
Zhang, Yong
and
Yuan, Peisen
2021.
Proof of a Dwork-type supercongruence by induction.
AIMS Mathematics,
Vol. 6,
Issue. 10,
p.
11568.
Sun, Zhi-Wei
2021.
Supercongruences involving Lucas sequences.
Monatshefte für Mathematik,
Vol. 196,
Issue. 3,
p.
577.
Guo, Victor J.W.
and
Zudilin, Wadim
2021.
Dwork-type supercongruences through a creative q-microscope.
Journal of Combinatorial Theory, Series A,
Vol. 178,
Issue. ,
p.
105362.
Ni, He-Xia
2021.
A q-Dwork-type generalization of Rodriguez-Villegas’ supercongruences.
Rocky Mountain Journal of Mathematics,
Vol. 51,
Issue. 6,
Wang, Chen
2021.
On two conjectural supercongruences of Z.-W. Sun.
The Ramanujan Journal,
Vol. 56,
Issue. 3,
p.
1111.
Mao, Guo-Shuai
and
Pan, Hao
2022.
Congruences corresponding to hypergeometric identities I. F12 transformations.
Journal of Mathematical Analysis and Applications,
Vol. 505,
Issue. 2,
p.
125527.
Mao, Guo-shuai
2022.
On a Supercongruence Conjecture of Z.-W. Sun.
Chinese Annals of Mathematics, Series B,
Vol. 43,
Issue. 3,
p.
417.
Li, Junhang
Tang, Yezhenyang
and
Wang, Chen
2023.
Some Congruences from the Karlsson-Minton Summation Formula.
Results in Mathematics,
Vol. 78,
Issue. 4,
Guo, Victor J. W.
and
Ni, He-Xia
2023.
Proof of some supercongruences through a q-microscope.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 4,
Guo, Victor J. W.
and
Ni, He-Xia
2023.
Further generalizations of four supercongruences of Rodriguez-Villegas.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 1,
Mao, Guo-Shuai
and
Pan, Hao
2025.
Congruences corresponding to hypergeometric identities II. Generalized hypergeometric transformations.
Bulletin des Sciences Mathématiques,
Vol. 199,
Issue. ,
p.
103570.