Hostname: page-component-6587cd75c8-rlsgg Total loading time: 0 Render date: 2025-04-23T16:01:51.403Z Has data issue: false hasContentIssue false
  • English
  • Français

CONGRUENCES FOR SUMS OF MACMAHON’S q-CATALAN POLYNOMIALS

Part of: Elementary number theory Sequences and sets Combinatorics

Published online by Cambridge University Press:  08 October 2024

TEWODROS AMDEBERHAN Open the ORCID record for TEWODROS AMDEBERHAN [Opens in a new window]  and
ROBERTO TAURASO Open the ORCID record for ROBERTO TAURASO [Opens in a new window]
TEWODROS AMDEBERHAN
Affiliation:
Department of Mathematics, Tulane University, New Orleans, LA 70118, USA e-mail: [email protected]
ROBERTO TAURASO*
Affiliation:
Dipartimento di Matematica, Università di Roma ‘Tor Vergata’, 00133 Roma, Italy
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

One variant of the q-Catalan polynomials is defined in terms of Gaussian polynomials by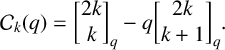

$$ \begin{align*}\mathcal{C}_k(q)=\bigg[\begin{matrix}{2k}\\ {k}\end{matrix}\bigg]_q-q \bigg[\begin{matrix}{2k}\\ {k+1} \end{matrix}\bigg]_q.\end{align*} $$

Liu [‘On a congruence involving q-Catalan numbers’, C. R. Math. Acad. Sci. Paris 358 (2020), 211–215] studied congruences of the form 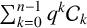$\sum _{k=0}^{n-1} q^k\mathcal {C}_k$ modulo the cyclotomic polynomial 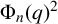$\Phi _n(q)^2$, provided that 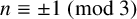$n\equiv \pm 1\pmod 3$. Apparently, the case 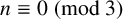$n\equiv 0\pmod 3$ has been missing from the literature. Our primary purpose is to fill this gap. In addition, we discuss a certain fascinating link to Dirichlet character sum identities.

Keywords

q-Catalan numberq-analogue congruenceq-binomial coefficientcyclotomic polynomialroots of unity

MSC classification

Primary: 11B65: Binomial coefficients; factorials; $q$-identities
Secondary: 05A10: Factorials, binomial coefficients, combinatorial functions 05A19: Combinatorial identities, bijective combinatorics 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Fürlinger, J. and Hofbauer, J., ‘ $q$ -Catalan numbers’, J. Combin. Theory Ser. A 40 (1985), 248–264.CrossRefGoogle Scholar
Liu, J.-C., ‘On a congruence involving $q$ -Catalan numbers’, C. R. Math. Acad. Sci. Paris 358 (2020), 211–215.CrossRefGoogle Scholar
Liu, J.-C. and Petrov, F., ‘Congruences on sums of $q$ -binomial coefficients’, Adv. Appl. Math. 116 (2020), 102003.CrossRefGoogle Scholar
MacMahon, P. A., Combinatory Analysis, 2 vols (Cambridge University Press, Cambridge, 1915–1916; reprinted by Chelsea, New York, 1960).Google Scholar
https://mathoverflow.net/questions/472815 .Google Scholar
Sagan, B. E., ‘Congruence properties of $q$ -analogs’, Adv. Math. 95 (1992), 127–143.CrossRefGoogle Scholar
Stanley, R. P., Catalan Numbers (Cambridge University Press, Cambridge, 2015).CrossRefGoogle Scholar
Tauraso, R., ‘ $q$ -analogs of some congruences involving Catalan numbers’, Adv. in Appl. Math. 48 (2012), 603–614.CrossRefGoogle Scholar
Tauraso, R., ‘Some $q$ -analogs of congruences for central binomial sums’, Colloq. Math. 133 (2013), 133–143.CrossRefGoogle Scholar