Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-02T11:04:59.443Z Has data issue: false hasContentIssue false
  • English
  • Français

CONDITIONS FOR A SCHUNCK CLASS TO BE A FORMATION

Part of: Lie algebras and Lie superalgebras General nonassociative rings Representation theory of groups

Published online by Cambridge University Press:  12 September 2014

DONALD W. BARNES
DONALD W. BARNES*
Affiliation:
1 Little Wonga Road, Cremorne, NSW 2090, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Schunck class 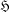$\mathfrak{H}$ is determined by the class 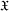$\mathfrak{X}$ of primitives contained in 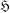$\mathfrak{H}$. We give necessary and sufficient conditions on 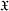$\mathfrak{X}$ for 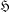$\mathfrak{H}$ to be a saturated formation.

Keywords

Lie algebrasformations

MSC classification

Primary: 17B30: Solvable, nilpotent (super)algebras
Secondary: 17A32: Leibniz algebras 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 69 - 75
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Barnes, D. W., ‘First cohomology groups of p-soluble groups’, J. Algebra 46 (1977), 298–302.CrossRefGoogle Scholar
Barnes, D. W., Schunck classes of restricted Lie algebras, arXiv:mathRA/0610609 (2006).Google Scholar
Barnes, D. W., ‘On locally defined formations of soluble Lie and Leibniz algebras’, Bull. Aust. Math. Soc. 86 (2012), 322–326.Google Scholar
Barnes, D. W., ‘Schunck classes of soluble Leibniz algebras’, Comm. Algebra 41 (2013), 4046–4065.CrossRefGoogle Scholar
Barnes, D. W., ‘Blocks of representations of Lie algebras’, arXiv:1405.4600 (2014).Google Scholar
Barnes, D. W. and Gastineau-Hills, H. M., ‘On the theory of soluble Lie algebras’, Math. Z. 106 (1968), 343–354.Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (de Gruyter, Berlin, New York, 1992).Google Scholar
Gaschütz, W., ‘Zur Theorie der endlichen auflösbaren Gruppen’, Math. Z. 80 (1963), 300–305.CrossRefGoogle Scholar