Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T12:12:51.513Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONDITIONAL DENSITY FOR CARMICHAEL NUMBERS

Part of: Elementary number theory Multiplicative number theory

Published online by Cambridge University Press:  13 February 2020

THOMAS WRIGHT
THOMAS WRIGHT*
Affiliation:
429 N. Church St., Spartanburg, SC29302, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Under sufficiently strong assumptions about the first prime in an arithmetic progression, we prove that the number of Carmichael numbers up to 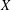$X$ is 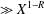$\gg X^{1-R}$, where 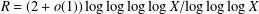$R=(2+o(1))\log \log \log \log X/\text{log}\log \log X$. This is close to Pomerance’s conjectured density of 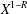$X^{1-R}$ with 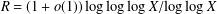$R=(1+o(1))\log \log \log X/\text{log}\log X$.

Keywords

Carmichael numberHeath-Brown conjectureleast prime in an arithmetic progression

MSC classification

Primary: 11A51: Factorization; primality
Secondary: 11N13: Primes in progressions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 379 - 388
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, W. R., Granville, A. and Pomerance, C., ‘There are infinitely many Carmichael numbers’, Ann. of Math. (2) 139(3) (1994), 703–722.CrossRefGoogle Scholar
Banks, W. D. and Pomerance, C., ‘On Carmichael numbers in arithmetic progressions’, J. Aust. Math. Soc. 88(3) (2010), 313–321.10.1017/S1446788710000169CrossRefGoogle Scholar
Carmichael, R. D., ‘Note on a new number theory function’, Bull. Am. Math. Soc. 16 (1910), 232–238.10.1090/S0002-9904-1910-01892-9CrossRefGoogle Scholar
Ekstrom, A., Pomerance, C. and Thakur, D. S., ‘Infinitude of elliptic Carmichael numbers’, J. Aust. Math. Soc. 92 (2012), 45–60.10.1017/S1446788712000080CrossRefGoogle Scholar
Erdős, P., ‘On pseudoprimes and Carmichael numbers’, Publ. Math. Debrecen 4 (1956), 201–206.Google Scholar
Harman, G., ‘Watt’s mean value theorem and Carmichael numbers’, Int. J. Number Theory 4(2) (2008), 241–248.CrossRefGoogle Scholar
Knödel, W., ‘Carmichaelsche Zahlen’, Math. Nachr. 9 (1953), 343–350.CrossRefGoogle Scholar
Korselt, A., ‘Problème chinois’, L’intermédiaire des mathématiciens 6 (1899), 142–143.Google Scholar
Meshulam, R., ‘An uncertainty inequality and zero subsums’, Discrete Math. 84(2) (1990), 197–200.10.1016/0012-365X(90)90375-RCrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I: Classical Theory (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Pomerance, C., ‘On the distribution of pseudoprimes’, Math. Comp. 37(156) (1981), 587–593.CrossRefGoogle Scholar
Šimerka, V., ‘Zbytky z arithmetické posloupnosti (On the remainders of an arithmetic progression)’, Časopis pro pěstováni matematiky a fysiky 14(5) (1885), 221–225.Google Scholar
Van Emde Boas, P. and Kruyswijk, D., A Combinatorial Problem on Finite Abelian Groups. III, Zuivere Wiskunde, 1969-008 (Stichting Mathematisch Centrum, Amsterdam, 1969).Google Scholar
Wright, T., ‘Infinitely many Carmichael numbers in arithmetic progressions’, Bull. Lond. Math. Soc. 45(5) (2013), 943–952.CrossRefGoogle Scholar
Wright, T., ‘Variants of Korselt’s criterion’, Canad. Math. Bull. 58(4) (2015), 869–876.10.4153/CMB-2015-027-3CrossRefGoogle Scholar
Wright, T., ‘There are infinitely many elliptic Carmichael numbers’, Bull. Lond. Math. Soc. 50(5) (2018), 791–800.CrossRefGoogle Scholar
Wright, T., ‘Factors of Carmichael numbers and an even weaker k-tuples conjecture’, Bull. Aust. Math. Soc. 99(3) (2019), 376–384.CrossRefGoogle Scholar