Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T19:54:12.813Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPLEXITY OF THOMASON’S ALGORITHM FOR FINDING A SECOND HAMILTONIAN CYCLE

Part of: Graph theory

Published online by Cambridge University Press:  03 May 2018

LIANG ZHONG Open the ORCID record for LIANG ZHONG [Opens in a new window]
LIANG ZHONG*
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian-Fuzhou, China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By Smith’s theorem, if a cubic graph has a Hamiltonian cycle, then it has a second Hamiltonian cycle. Thomason [‘Hamilton cycles and uniquely edge-colourable graphs’, Ann. Discrete Math.3 (1978), 259–268] gave a simple algorithm to find the second cycle. Thomassen [private communication] observed that if there exists a polynomially bounded algorithm for finding a second Hamiltonian cycle in a cubic cyclically 4-edge connected graph 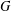$G$, then there exists a polynomially bounded algorithm for finding a second Hamiltonian cycle in any cubic graph 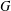$G$. In this paper we present a class of cyclically 4-edge connected cubic bipartite graphs 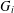$G_{i}$ with $16(i+1)$ vertices such that Thomason’s algorithm takes $12(2^{i}-1)+3$ steps to find a second Hamiltonian cycle in 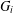$G_{i}$.

Keywords

Hamiltonian cyclelollipop method

MSC classification

Primary: 05C45: Eulerian and Hamiltonian graphs
Secondary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 18 - 26
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Cameron, K., ‘Thomason’s algorithm for finding a second hamiltonian circuit through a given edge in a cubic graph is exponential on Krawczyk’s graphs’, Discrete Math. 235 (2001), 69–77.CrossRefGoogle Scholar
Karp, R. M., ‘Reducibility among combinatorial problems’, in: Complexity of Computer Computations (eds. Miller, R. E., Thatcher, J. W. and Bohlinger, J. D.) (Plenum Press, New York, 1972), 85–103.CrossRefGoogle Scholar
Krawczyk, A., ‘The complexity of finding a second Hamiltonian cycle in cubic graphs’, J. Comput. Systems Sci. 58 (1999), 641–647.Google Scholar
Thomason, A. G., ‘Hamilton cycles and uniquely edge-colourable graphs’, Ann. Discrete Math. 3 (1978), 259–268.Google Scholar
Tutte, W. T., ‘On Hamiltonian circuits’, J. Lond. Math. Soc. 21 (1946), 98–101.Google Scholar