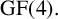1 Introduction
Weighing matrices (to be defined below) constitute a far reaching generalisation of Hadamard matrices [Reference Egan10]. Several databases are available on the internet [Reference Bruzda, Tadej and Życzkowski5, Reference Harada and Munemasa13]. In this note, we consider such matrices over the cubic and sextic complex roots of unity [Reference Best, Kharaghani and Ramp3]. Note that the quotient of the Eisenstein integers by the ideal generated by
![]() $2$
is equal to
$2$
is equal to
![]() $\mathrm {GF}(4).$
In view of that well-known arithmetic fact, it is natural to construct quaternary codes from such weighing matrices. In this note, we construct Hermitian quaternary self-dual codes by extending two constructions of binary self-dual codes [Reference Armario and Frau1, Reference Harada12] to quaternary codes. The two families of codes are called
$\mathrm {GF}(4).$
In view of that well-known arithmetic fact, it is natural to construct quaternary codes from such weighing matrices. In this note, we construct Hermitian quaternary self-dual codes by extending two constructions of binary self-dual codes [Reference Armario and Frau1, Reference Harada12] to quaternary codes. The two families of codes are called
![]() $C_{n,k}$
and
$C_{n,k}$
and
![]() $C^*_{n,k},$
where n stands for the order of the weighing matrix and k for its weight. In addition to being of interest in their own right, Hermitian quaternary codes that are self-orthogonal are used in the construction of quantum error-correcting codes (see [Reference Calderbank, Rains, Shor and Sloane6]). Further, since
$C^*_{n,k},$
where n stands for the order of the weighing matrix and k for its weight. In addition to being of interest in their own right, Hermitian quaternary codes that are self-orthogonal are used in the construction of quantum error-correcting codes (see [Reference Calderbank, Rains, Shor and Sloane6]). Further, since
![]() $4$
is the smallest square prime power greater than
$4$
is the smallest square prime power greater than
![]() $1$
, Hermitian quaternary self-dual codes have been the first and the most studied amongst Hermitian self-dual codes (see [Reference MacWilliams, Odlyzko, Sloane and Ward15]). The second construction requires Hermitian weighing matrices. Such objects are not classical and a generation technique, of independent interest, is described.
$1$
, Hermitian quaternary self-dual codes have been the first and the most studied amongst Hermitian self-dual codes (see [Reference MacWilliams, Odlyzko, Sloane and Ward15]). The second construction requires Hermitian weighing matrices. Such objects are not classical and a generation technique, of independent interest, is described.
In the same vein, we construct Hermitian linear complementary dual (shortly LCD) codes over
![]() $\mathrm {GF}(4)$
in the sense of [Reference Crnković, Egan, Rodrigues and Švob8]. The two types of codes obtained are called
$\mathrm {GF}(4)$
in the sense of [Reference Crnković, Egan, Rodrigues and Švob8]. The two types of codes obtained are called
![]() $L_{n,k}$
and
$L_{n,k}$
and
![]() $L^*_{n,k},$
where n stands for the order of the weighing matrix and k for its weight. A new method for constructing Hermitian LCD codes is also introduced in [Reference Li, Shi and Liu14]. We believe that the codes generated using the construction methods in this paper can serve as invariants of such matrices from a classification perspective. This is in the spirit of the classification of designs by their codes in the famous book [Reference Assmus and Key2].
$L^*_{n,k},$
where n stands for the order of the weighing matrix and k for its weight. A new method for constructing Hermitian LCD codes is also introduced in [Reference Li, Shi and Liu14]. We believe that the codes generated using the construction methods in this paper can serve as invariants of such matrices from a classification perspective. This is in the spirit of the classification of designs by their codes in the famous book [Reference Assmus and Key2].
The material is arranged as follows. The next section collects the notions and notation needed for the rest of the paper. Sections 3 and 4 study Hermitian quaternary self-dual codes and Hermitian LCD codes. In Section 5, an algorithm is presented for finding Hermitian matrices in the equivalence class of
![]() $\mathit {CW}(n,k,q)$
. Section 6 contains numerical examples of these constructions.
$\mathit {CW}(n,k,q)$
. Section 6 contains numerical examples of these constructions.
2 Notation and definitions
2.1 Codes
An
![]() $[n,k]$
linear code C over
$[n,k]$
linear code C over
![]() $\mathrm {GF}(q)$
is a k-dimensional vector subspace of
$\mathrm {GF}(q)$
is a k-dimensional vector subspace of
![]() $\mathrm {GF}(q)^n,$
where
$\mathrm {GF}(q)^n,$
where
![]() $\mathrm {GF}(q)$
denotes the Galois field of order
$\mathrm {GF}(q)$
denotes the Galois field of order
![]() $q,$
with q being a power of a prime
$q,$
with q being a power of a prime
![]() $p.$
The elements in C are called codewords and the weight
$p.$
The elements in C are called codewords and the weight
![]() $wt(x)$
of a codeword x is the number of its nonzero coordinates. The distance between two codewords x and y is the weight
$wt(x)$
of a codeword x is the number of its nonzero coordinates. The distance between two codewords x and y is the weight
![]() $wt(x-y).$
The minimum weight of a linear code C is defined as
$wt(x-y).$
The minimum weight of a linear code C is defined as
![]() $\min \{ wt(x) \mid 0 \ne x\in C \} .$
An
$\min \{ wt(x) \mid 0 \ne x\in C \} .$
An
![]() $[n,k,d]$
code is a linear code with minimum weight
$[n,k,d]$
code is a linear code with minimum weight
![]() $d.$
If there exists an n-order monomial matrix P over
$d.$
If there exists an n-order monomial matrix P over
![]() $\mathrm {GF}(q)$
such that
$\mathrm {GF}(q)$
such that
![]() $C'=CP= \{ cP \mid c\in C \},$
then the codes C and
$C'=CP= \{ cP \mid c\in C \},$
then the codes C and
![]() $C'$
over
$C'$
over
![]() $\mathrm {GF}(q)$
are said to be equivalent. If
$\mathrm {GF}(q)$
are said to be equivalent. If
![]() $C=CP$
holds,
$C=CP$
holds,
![]() $CP$
is referred to as an automorphism of C and the set of all automorphisms of C forms the automorphism group of C. Let
$CP$
is referred to as an automorphism of C and the set of all automorphisms of C forms the automorphism group of C. Let
![]() $\mathrm {GF}(4)= \{ 0,1,v,v+1 \} $
be a finite field of order
$\mathrm {GF}(4)= \{ 0,1,v,v+1 \} $
be a finite field of order
![]() $4.$
The Hermitian inner product between codewords
$4.$
The Hermitian inner product between codewords
![]() ${x=(x_1,x_2,\ldots ,x_n)}$
and
${x=(x_1,x_2,\ldots ,x_n)}$
and
![]() $y=(y_1,y_2,\ldots ,y_n)$
is defined as
$y=(y_1,y_2,\ldots ,y_n)$
is defined as
![]() $x\cdot y=\sum _{i=1}^{n} x_i y_i^2.$
The Hermitian dual code
$x\cdot y=\sum _{i=1}^{n} x_i y_i^2.$
The Hermitian dual code
![]() $C^{\perp _H}$
is defined as
$C^{\perp _H}$
is defined as
![]() $C^{\perp _H}= \{ x\in \mathrm {GF}(4)^n \mid x\cdot y=0 \mbox { for all } y\in C \}$
. If
$C^{\perp _H}= \{ x\in \mathrm {GF}(4)^n \mid x\cdot y=0 \mbox { for all } y\in C \}$
. If
![]() $C\subseteq C^{\perp _H},$
then C is Hermitian self-orthogonal, and Hermitian self-dual if
$C\subseteq C^{\perp _H},$
then C is Hermitian self-orthogonal, and Hermitian self-dual if
![]() $C=C^{\perp _H}.$
A table of Hermitian self-dual codes over
$C=C^{\perp _H}.$
A table of Hermitian self-dual codes over
![]() $\mathrm {GF}(4)$
is provided in [Reference Gaborit11], where for a given length, the highest bound is given. If a Hermitian self-dual code meets this bound, it is considered optimal. A linear code C over
$\mathrm {GF}(4)$
is provided in [Reference Gaborit11], where for a given length, the highest bound is given. If a Hermitian self-dual code meets this bound, it is considered optimal. A linear code C over
![]() $\mathrm {GF}(4)$
is usually called a Hermitian LCD code if
$\mathrm {GF}(4)$
is usually called a Hermitian LCD code if
![]() $C\cap C^{\perp _H}= \{ 0 \} .$
$C\cap C^{\perp _H}= \{ 0 \} .$
2.2 Combinatorial matrices
A complex weighing matrix
![]() $W\in \mathit {CW}(n,k,q)$
is a matrix of order n and weight
$W\in \mathit {CW}(n,k,q)$
is a matrix of order n and weight
![]() $k.$
Its elements are
$k.$
Its elements are
![]() $0$
and the qth roots of unity
$0$
and the qth roots of unity
![]() $\zeta _q,$
and it satisfies
$\zeta _q,$
and it satisfies
![]() $WW^*=kI_n,$
where
$WW^*=kI_n,$
where
![]() $k\le n.$
Here,
$k\le n.$
Here,
![]() $W^*$
denotes the conjugate transpose of W and
$W^*$
denotes the conjugate transpose of W and
![]() $I_n$
is the
$I_n$
is the
![]() $n\times n$
identity matrix. The set
$n\times n$
identity matrix. The set
![]() $\mathit {CW}(n,n,q)$
corresponds to the set of Butson–Hadamard matrices,
$\mathit {CW}(n,n,q)$
corresponds to the set of Butson–Hadamard matrices,
![]() $BH(n,q).$
For
$BH(n,q).$
For
![]() $q=3,$
the complex weighing matrix
$q=3,$
the complex weighing matrix
![]() $W\in \mathit {CW}(n,k,3)$
includes elements
$W\in \mathit {CW}(n,k,3)$
includes elements
![]() $0,1,\zeta _3$
and
$0,1,\zeta _3$
and
![]() $\zeta _3^2.$
For
$\zeta _3^2.$
For
![]() $q=6,$
the complex weighing matrix
$q=6,$
the complex weighing matrix
![]() $W\in \mathit {CW}(n,k,6)$
includes elements
$W\in \mathit {CW}(n,k,6)$
includes elements
![]() $0,1,\zeta _6,\zeta _6^2,-1,-\zeta _6$
and
$0,1,\zeta _6,\zeta _6^2,-1,-\zeta _6$
and
![]() $-\zeta _6^2.$
In this paper, we focus on the codes generated by these two types of matrices over
$-\zeta _6^2.$
In this paper, we focus on the codes generated by these two types of matrices over
![]() $\mathrm {GF}(4).$
It is natural to study complex weighing matrices in the context of constructing codes rather than the full weight Butson–Hadamard matrices for two reasons. The first is that when interpreted over
$\mathrm {GF}(4).$
It is natural to study complex weighing matrices in the context of constructing codes rather than the full weight Butson–Hadamard matrices for two reasons. The first is that when interpreted over
![]() $\mathrm { GF}(4)$
, it is natural to allow for entries equal to
$\mathrm { GF}(4)$
, it is natural to allow for entries equal to
![]() $0$
. However, more importantly, nontrivial complex weighing matrices may exist when Butson matrices cannot. This is particularly apparent in the case of
$0$
. However, more importantly, nontrivial complex weighing matrices may exist when Butson matrices cannot. This is particularly apparent in the case of
![]() $\mathit { CW}(n,k,3)$
as it is not a requirement that
$\mathit { CW}(n,k,3)$
as it is not a requirement that
![]() $3 \mid n$
when
$3 \mid n$
when
![]() $k < n$
. Additionally, for any n, one can construct at least one
$k < n$
. Additionally, for any n, one can construct at least one
![]() $\mathit {CW}(n,k,6)$
with
$\mathit {CW}(n,k,6)$
with
![]() $2 \leq k \leq n$
. See [Reference Egan10] and the references contained therein for further details on complex weighing matrices and their existence.
$2 \leq k \leq n$
. See [Reference Egan10] and the references contained therein for further details on complex weighing matrices and their existence.
If there exist two monomial matrices P and
![]() $Q,$
where the nonzero entries of P and Q are qth roots of unity, such that
$Q,$
where the nonzero entries of P and Q are qth roots of unity, such that
![]() $W'=PWQ^*,$
then we say that the two complex weighing matrices W and
$W'=PWQ^*,$
then we say that the two complex weighing matrices W and
![]() $W',$
both of order n and weight
$W',$
both of order n and weight
![]() $k,$
with nonzero entries that are qth roots of unity, are equivalent and we write
$k,$
with nonzero entries that are qth roots of unity, are equivalent and we write
![]() $W\equiv W'.$
If
$W\equiv W'.$
If
![]() $W'=PWQ^*$
holds,
$W'=PWQ^*$
holds,
![]() $W'$
is referred to as an automorphism of
$W'$
is referred to as an automorphism of
![]() $W.$
The set of all automorphisms of W forms the automorphism group of
$W.$
The set of all automorphisms of W forms the automorphism group of
![]() $W.$
$W.$
3 Hermitian self-dual codes over
 $\mathrm {GF}(4)$
$\mathrm {GF}(4)$
In this section, we present two methods for constructing Hermitian self-dual codes over
![]() $\mathrm {GF}(4)$
using complex weighing matrices.
$\mathrm {GF}(4)$
using complex weighing matrices.
Theorem 3.1. Let
![]() $W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix satisfying
$W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix satisfying
![]() ${k \equiv 1 \pmod {2}.}$
If
${k \equiv 1 \pmod {2}.}$
If
![]() $\alpha $
is a nonzero element in
$\alpha $
is a nonzero element in
![]() $\mathrm {GF}(4),$
then the matrix
$\mathrm {GF}(4),$
then the matrix
![]() $ G=[\begin {matrix} \alpha I_n & W \end {matrix}] $
generates a Hermitian self-dual
$ G=[\begin {matrix} \alpha I_n & W \end {matrix}] $
generates a Hermitian self-dual
![]() $[2n,n]$
code
$[2n,n]$
code
![]() $C_{n,k}$
over
$C_{n,k}$
over
![]() $\mathrm {GF}(4).$
The matrix
$\mathrm {GF}(4).$
The matrix
![]() ${G'=[\begin {matrix} \alpha I_n & W' \end {matrix}]}$
also generates a Hermitian self-dual
${G'=[\begin {matrix} \alpha I_n & W' \end {matrix}]}$
also generates a Hermitian self-dual
![]() $[2n,n]$
code over
$[2n,n]$
code over
![]() $\mathrm {GF}(4),$
where
$\mathrm {GF}(4),$
where
![]() $W'$
is equivalent to
$W'$
is equivalent to
![]() $W.$
$W.$
Proof. Consider the equation
![]() $GG^*=\alpha \overline {\alpha }I_n+WW^*=I_n+kI_n=(k+1)I_n=0,$
where
$GG^*=\alpha \overline {\alpha }I_n+WW^*=I_n+kI_n=(k+1)I_n=0,$
where
![]() $\overline {\alpha }$
denotes the complex conjugate of
$\overline {\alpha }$
denotes the complex conjugate of
![]() $\alpha .$
If
$\alpha .$
If
![]() $W'$
is equivalent to
$W'$
is equivalent to
![]() $W,$
then
$W,$
then
![]() $W'W^{\prime *}=kI_n,$
which implies
$W'W^{\prime *}=kI_n,$
which implies
![]() $G'G^{\prime *}=0.$
Therefore,
$G'G^{\prime *}=0.$
Therefore,
![]() $G'$
also generates a Hermitian self-dual code, as required.
$G'$
also generates a Hermitian self-dual code, as required.
Theorem 3.2. Let
![]() $W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix that satisfies
$W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix that satisfies
![]() $k \equiv 0 \pmod {2}$
and
$k \equiv 0 \pmod {2}$
and
![]() $W=W^*.$
If
$W=W^*.$
If
![]() $\alpha $
is a nonzero element in
$\alpha $
is a nonzero element in
![]() $\mathrm {GF}(4),$
then the matrix
$\mathrm {GF}(4),$
then the matrix
![]() $ G=[\begin {matrix} \alpha I_n & I_n+W \end {matrix}] $
generates a Hermitian self-dual
$ G=[\begin {matrix} \alpha I_n & I_n+W \end {matrix}] $
generates a Hermitian self-dual
![]() $[2n,n]$
code
$[2n,n]$
code
![]() $C^*_{n,k}$
over
$C^*_{n,k}$
over
![]() $\mathrm {GF}(4).$
The matrix
$\mathrm {GF}(4).$
The matrix
![]() $G'=[\begin {matrix} \alpha I_n & I_n+W' \end {matrix}]$
also generates a Hermitian self-dual
$G'=[\begin {matrix} \alpha I_n & I_n+W' \end {matrix}]$
also generates a Hermitian self-dual
![]() $[2n,n]$
code over
$[2n,n]$
code over
![]() $\mathrm {GF}(4),$
where
$\mathrm {GF}(4),$
where
![]() $W'=W^{\prime *}$
and
$W'=W^{\prime *}$
and
![]() $W'$
is equivalent to
$W'$
is equivalent to
![]() $W.$
$W.$
Proof. The product
![]() $GG^*$
yields
$GG^*$
yields
![]() $\alpha \bar {\alpha }I_n+I_n+ W^*+W+WW^*.$
Since W is a complex weighing matrix, it satisfies
$\alpha \bar {\alpha }I_n+I_n+ W^*+W+WW^*.$
Since W is a complex weighing matrix, it satisfies
![]() $WW^*=kI_n.$
Considering
$WW^*=kI_n.$
Considering
![]() $k \equiv 0 \pmod {2}$
and
$k \equiv 0 \pmod {2}$
and
![]() $W=W^*,$
this simplifies to
$W=W^*,$
this simplifies to
![]() $GG^*=0.$
Similarly, when
$GG^*=0.$
Similarly, when
![]() $W'=W^{\prime *}$
and
$W'=W^{\prime *}$
and
![]() $W'$
is equivalent to
$W'$
is equivalent to
![]() $W,$
the same conclusion can be drawn.
$W,$
the same conclusion can be drawn.
Proposition 3.3. If W and
![]() $W'$
are equivalent complex weighing matrices of order n and weight
$W'$
are equivalent complex weighing matrices of order n and weight
![]() $k,$
then the Hermitian self-dual codes constructed from W and
$k,$
then the Hermitian self-dual codes constructed from W and
![]() $W'$
by Theorem 3.1 are also equivalent.
$W'$
by Theorem 3.1 are also equivalent.
Proof. Since W and
![]() $W'$
are equivalent, there exist monomial matrices P and Q such that
$W'$
are equivalent, there exist monomial matrices P and Q such that
![]() $W'=PWQ^*.$
Therefore,
$W'=PWQ^*.$
Therefore,
 $$ \begin{align*} [\begin{matrix} \alpha I_n & W' \end{matrix}]=[\begin{matrix} \alpha I_n & PWQ^* \end{matrix}]=P[\begin{matrix} \alpha I_n & W \end{matrix}]\begin{bmatrix} P^{-1} & \mathbf{0}\\ \mathbf{0} & Q^* \end{bmatrix}, \end{align*} $$
$$ \begin{align*} [\begin{matrix} \alpha I_n & W' \end{matrix}]=[\begin{matrix} \alpha I_n & PWQ^* \end{matrix}]=P[\begin{matrix} \alpha I_n & W \end{matrix}]\begin{bmatrix} P^{-1} & \mathbf{0}\\ \mathbf{0} & Q^* \end{bmatrix}, \end{align*} $$
where the matrix
![]() $[\begin {smallmatrix} P^{-1} & \mathbf {0}\\ \mathbf {0} & Q^* \end {smallmatrix}]$
is a
$[\begin {smallmatrix} P^{-1} & \mathbf {0}\\ \mathbf {0} & Q^* \end {smallmatrix}]$
is a
![]() $2n\times 2n$
monomial matrix and
$2n\times 2n$
monomial matrix and
![]() $\mathbf {0}$
denotes the
$\mathbf {0}$
denotes the
![]() $n\times n$
zero matrix. This completes the proof.
$n\times n$
zero matrix. This completes the proof.
4 Hermitian LCD codes over
 $\mathrm {GF}(4)$
$\mathrm {GF}(4)$
In this section, two methods are presented for constructing Hermitian LCD codes over
![]() $\mathrm {GF}(4)$
using complex weighing matrices.
$\mathrm {GF}(4)$
using complex weighing matrices.
Proposition 4.1 [Reference Carlet, Mesnager, Tang and Qi7, Proposition 2].
If G is a generator matrix for the
![]() $[n,k]$
linear code
$[n,k]$
linear code
![]() $C,$
then the
$C,$
then the
![]() $k\times k$
matrix
$k\times k$
matrix
![]() $GG^*$
is nonsingular if and only if C is a Hermitian LCD code.
$GG^*$
is nonsingular if and only if C is a Hermitian LCD code.
Theorem 4.2. Let
![]() $W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix with k even. If
$W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix with k even. If
![]() $\alpha $
is a nonzero element in
$\alpha $
is a nonzero element in
![]() $\mathrm {GF}(4),$
then the matrix
$\mathrm {GF}(4),$
then the matrix
![]() $ G=[\begin {matrix} \alpha I_n & W \end {matrix}] $
generates a Hermitian LCD code
$ G=[\begin {matrix} \alpha I_n & W \end {matrix}] $
generates a Hermitian LCD code
![]() $L_{n,k} $
of length
$L_{n,k} $
of length
![]() $2n$
over
$2n$
over
![]() $\mathrm {GF}(4).$
$\mathrm {GF}(4).$
Proof. From the proof of Theorem 3.1,
![]() $GG^*=(k+1)I_n,$
and hence
$GG^*=(k+1)I_n,$
and hence
![]() $\det (GG^*)=(k+1)^n.$
Then the claim follows from Proposition 4.1.
$\det (GG^*)=(k+1)^n.$
Then the claim follows from Proposition 4.1.
Theorem 4.3. Let
![]() $W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix with k odd and
$W\in \mathit {CW}(n,k,q)$
be a complex weighing matrix with k odd and
![]() $W=W^*.$
If
$W=W^*.$
If
![]() $\alpha $
is a nonzero element in
$\alpha $
is a nonzero element in
![]() $\mathrm {GF}(4),$
then the matrix
$\mathrm {GF}(4),$
then the matrix
![]() $ G=[\begin {matrix} \alpha I_n & I_n+W \end {matrix}] $
generates a Hermitian LCD code
$ G=[\begin {matrix} \alpha I_n & I_n+W \end {matrix}] $
generates a Hermitian LCD code
![]() $L^*_{n,k}$
of length
$L^*_{n,k}$
of length
![]() $2n$
over
$2n$
over
![]() $\mathrm {GF}(4).$
$\mathrm {GF}(4).$
Proof. From the proof of Theorem 3.2, it follows that
![]() $GG^*=(k+2)I_n,$
and hence
$GG^*=(k+2)I_n,$
and hence
![]() $\det (GG^*)=(k+2)^n.$
Then, the result is obtained from Proposition 4.1.
$\det (GG^*)=(k+2)^n.$
Then, the result is obtained from Proposition 4.1.
Remark 4.4. In Theorem 4.2, if
![]() $W'$
is equivalent to
$W'$
is equivalent to
![]() $W,$
then the same construction will also generate a Hermitian LCD code of length
$W,$
then the same construction will also generate a Hermitian LCD code of length
![]() $2n$
over
$2n$
over
![]() $\mathrm {GF}(4).$
Furthermore, the Hermitian LCD code generated by
$\mathrm {GF}(4).$
Furthermore, the Hermitian LCD code generated by
![]() $W'$
is equivalent to the Hermitian LCD code generated by W. Similarly, in Theorem 4.3, if
$W'$
is equivalent to the Hermitian LCD code generated by W. Similarly, in Theorem 4.3, if
![]() $W'$
is an equivalent Hermitian matrix to
$W'$
is an equivalent Hermitian matrix to
![]() $W,$
then the same construction method will generate a Hermitian LCD code over
$W,$
then the same construction method will generate a Hermitian LCD code over
![]() $\mathrm { GF}(4).$
$\mathrm { GF}(4).$
5 Finding Hermitian matrices in the equivalence class of a
 $\mathit {CW}(n,k,q)$
$\mathit {CW}(n,k,q)$
Let
![]() $\mathrm {Mon}_{n}(q)$
be the group of
$\mathrm {Mon}_{n}(q)$
be the group of
![]() $n \times n$
monomial matrices with nonzero entries in the qth roots of unity. The group
$n \times n$
monomial matrices with nonzero entries in the qth roots of unity. The group
![]() $\mathrm {Mon}_{n}(q)^{2}$
acts on
$\mathrm {Mon}_{n}(q)^{2}$
acts on
![]() $\mathit {CW}(n,k,q)$
via
$\mathit {CW}(n,k,q)$
via
The orbits under this action are the equivalence classes. Restricting to the action of the group
![]() $\mathrm {Mon}_{n}(1)^{2}$
, the orbits are permutation equivalence classes. The stabilisers of a matrix W under these actions are the automorphism and permutation automorphism groups. Our next goal is to describe an algorithm for searching through the equivalence class of a given
$\mathrm {Mon}_{n}(1)^{2}$
, the orbits are permutation equivalence classes. The stabilisers of a matrix W under these actions are the automorphism and permutation automorphism groups. Our next goal is to describe an algorithm for searching through the equivalence class of a given
![]() $\mathit {CW}(n,k,q)$
for Hermitian members. That is, given
$\mathit {CW}(n,k,q)$
for Hermitian members. That is, given
![]() $W \in {\mathit {CW}}(n,k,q)$
, we search for a matrix
$W \in {\mathit {CW}}(n,k,q)$
, we search for a matrix
![]() $H \equiv W$
such that
$H \equiv W$
such that
![]() $H = H^{\ast }$
.
$H = H^{\ast }$
.
For any Hermitian matrix H, it must be true that
![]() $H_{ij} = 0$
if and only if
$H_{ij} = 0$
if and only if
![]() $H_{ji} = 0$
. Given any
$H_{ji} = 0$
. Given any
![]() $W \in \mathit {CW}(n,k,q)$
, let
$W \in \mathit {CW}(n,k,q)$
, let
![]() $W_{c}$
denote the matrix obtained from W by letting the
$W_{c}$
denote the matrix obtained from W by letting the
![]() $(i,j)$
entry be
$(i,j)$
entry be
![]() $1$
if
$1$
if
![]() $W_{ij} = c$
, and
$W_{ij} = c$
, and
![]() $0$
otherwise. Adhering to this notation,
$0$
otherwise. Adhering to this notation,
 $$ \begin{align*} W = \sum_{c \in \{0\}\cup \langle \zeta_{q} \rangle}cW_{c}. \end{align*} $$
$$ \begin{align*} W = \sum_{c \in \{0\}\cup \langle \zeta_{q} \rangle}cW_{c}. \end{align*} $$
In particular, the matrix
![]() $W_{0}$
is a
$W_{0}$
is a
![]() $(0,1)$
-matrix of weight
$(0,1)$
-matrix of weight
![]() $n-k$
and, if W is Hermitian, then
$n-k$
and, if W is Hermitian, then
![]() $W_{0}$
is symmetric. The following proposition is immediate.
$W_{0}$
is symmetric. The following proposition is immediate.
Proposition 5.1. If there exists a Hermitian matrix in the equivalence class of W, then the matrix
![]() $W_{0}$
is permutation equivalent to a symmetric matrix.
$W_{0}$
is permutation equivalent to a symmetric matrix.
We now make another simple observation. Suppose that
![]() $H \in \mathit {CW}(n,k,q)$
is Hermitian. For any
$H \in \mathit {CW}(n,k,q)$
is Hermitian. For any
![]() $M \in \mathrm {Mon}_{n}(q),$
we observe that
$M \in \mathrm {Mon}_{n}(q),$
we observe that
Hence,
![]() $MHM^{\ast }$
is also Hermitian for any choice of M. Suppose now that W is any matrix in
$MHM^{\ast }$
is also Hermitian for any choice of M. Suppose now that W is any matrix in
![]() $\mathit {CW}(n,k,q)$
, not necessarily Hermitian, that is equivalent to H. Then, there exist matrices
$\mathit {CW}(n,k,q)$
, not necessarily Hermitian, that is equivalent to H. Then, there exist matrices
![]() $S,T \in \mathrm {Mon}_{n}(q)$
such that
$S,T \in \mathrm {Mon}_{n}(q)$
such that
![]() $SWT^{\ast } = H$
. It follows that
$SWT^{\ast } = H$
. It follows that
![]() $T^{\ast }SW = T^{\ast }HT$
, which is Hermitian by (5.1). The next proposition follows immediately.
$T^{\ast }SW = T^{\ast }HT$
, which is Hermitian by (5.1). The next proposition follows immediately.
Proposition 5.2. Let
![]() $W \in \mathit {CW}(n,k,q)$
and suppose that there is a Hermitian matrix H in the equivalence class of W. Then, there is a monomial matrix
$W \in \mathit {CW}(n,k,q)$
and suppose that there is a Hermitian matrix H in the equivalence class of W. Then, there is a monomial matrix
![]() $M \in \mathrm {Mon}_{n}(q)$
such that
$M \in \mathrm {Mon}_{n}(q)$
such that
![]() $MW$
is Hermitian.
$MW$
is Hermitian.
It follows that if there is a Hermitian
![]() $H \equiv W$
, we need only search for M such that
$H \equiv W$
, we need only search for M such that
![]() $MW$
is Hermitian. Now, we may write any matrix
$MW$
is Hermitian. Now, we may write any matrix
![]() $M \in \mathrm {Mon}_{n}(q)$
uniquely in the form
$M \in \mathrm {Mon}_{n}(q)$
uniquely in the form
![]() $M = DP,$
where D is diagonal and P is a permutation matrix. If
$M = DP,$
where D is diagonal and P is a permutation matrix. If
![]() $MW$
is Hermitian, then it follows that
$MW$
is Hermitian, then it follows that
![]() $PW_{0}$
is symmetric.
$PW_{0}$
is symmetric.
Suppose now that a matrix
![]() $W \in \mathit {CW}(n,k,q)$
is given. We first want to determine whether or not there exists a Hermitian matrix in the equivalence class of W, and then find these Hermitian matrices in case they exist. Proposition 5.2 allows us to consider only the orbit of W under the action of
$W \in \mathit {CW}(n,k,q)$
is given. We first want to determine whether or not there exists a Hermitian matrix in the equivalence class of W, and then find these Hermitian matrices in case they exist. Proposition 5.2 allows us to consider only the orbit of W under the action of
![]() $\mathrm {Mon}_{n}(q)$
via left multiplication. A matrix in
$\mathrm {Mon}_{n}(q)$
via left multiplication. A matrix in
![]() $\mathit {CW}(n,k,q)$
is normalised if the first nonzero entry in every row and column is
$\mathit {CW}(n,k,q)$
is normalised if the first nonzero entry in every row and column is
![]() $1$
. Any matrix is diagonally equivalent to a normalised matrix.
$1$
. Any matrix is diagonally equivalent to a normalised matrix.
Proposition 5.3. Let
![]() $H \in \mathit {CW}(n,k,q)$
be Hermitian. Then, there exists a diagonal matrix D such that
$H \in \mathit {CW}(n,k,q)$
be Hermitian. Then, there exists a diagonal matrix D such that
![]() $DHD^{\ast }$
is normalised and Hermitian.
$DHD^{\ast }$
is normalised and Hermitian.
Proof. Let
![]() $D_{j}$
be the diagonal matrix with
$D_{j}$
be the diagonal matrix with
![]() $\overline {H_{ij}}$
in the ith position of the diagonal, if
$\overline {H_{ij}}$
in the ith position of the diagonal, if
![]() $H_{ij}$
is the first nonzero entry in row j, and
$H_{ij}$
is the first nonzero entry in row j, and
![]() $1$
elsewhere on the diagonal. Set
$1$
elsewhere on the diagonal. Set
![]() ${D = D_{n}D_{n-1}\cdots D_{2}D_{1}}$
. Then, the matrix
${D = D_{n}D_{n-1}\cdots D_{2}D_{1}}$
. Then, the matrix
![]() $DHD^{\ast }$
is normalised and also Hermitian by (5.1).
$DHD^{\ast }$
is normalised and also Hermitian by (5.1).
It follows from Proposition 5.3 that if
![]() $W \in \mathit {CW}(n,k,q)$
is diagonally equivalent to a Hermitian matrix, then there exist diagonal matrices D and E such that
$W \in \mathit {CW}(n,k,q)$
is diagonally equivalent to a Hermitian matrix, then there exist diagonal matrices D and E such that
![]() $DWE^{\ast }$
is both normalised and Hermitian.
$DWE^{\ast }$
is both normalised and Hermitian.
Combining the details of the section up to now, we describe a simple computational algorithm for finding a Hermitian matrix, if it exists, in the equivalence class of a given matrix
![]() $W \in \mathit {CW}(n,k,q)$
.
$W \in \mathit {CW}(n,k,q)$
.
-
(1) Given W, construct
 $W_{0}$
.
$W_{0}$
. -
(2) Find a single permutation matrix
 $Q \in \mathrm {Mon}_{n}(1)$
such that
$Q \in \mathrm {Mon}_{n}(1)$
such that
 $QW_{0}$
is symmetric.
$QW_{0}$
is symmetric. -
(3) Find all permutation matrices
 $P \in \mathrm {Mon}_{n}(1)$
such that
$P \in \mathrm {Mon}_{n}(1)$
such that
 $PW_{0}$
is symmetric.
$PW_{0}$
is symmetric. -
(4) For each P found in the previous step, find pairs of diagonal matrices D and E so that the matrix
 $H = D(PW)E^{\ast }$
is normalised. If H is Hermitian, then exit the algorithm.
$H = D(PW)E^{\ast }$
is normalised. If H is Hermitian, then exit the algorithm.
Steps (1) and (4) of this algorithm are straightforward, requiring no significant computational effort. Step (2) is computationally difficult, and represents the most time-consuming aspect of the algorithm. Fortunately, searching through all of
![]() $\mathrm {Mon}_{n}(1)$
for the matrix Q is not necessary. This is because any assumption that row i of
$\mathrm {Mon}_{n}(1)$
for the matrix Q is not necessary. This is because any assumption that row i of
![]() $W_{0}$
is permuted to row j immediately restricts the search space, as the remaining rows must be permuted so as to preserve symmetry. For example, if the first row of
$W_{0}$
is permuted to row j immediately restricts the search space, as the remaining rows must be permuted so as to preserve symmetry. For example, if the first row of
![]() $W_{0}$
is fixed, then the
$W_{0}$
is fixed, then the
![]() $1$
s on the first column must be preserved. Any subsequent assumptions have a similar effect. For the values of n considered in this work, very few assumptions are required before complete searches through remaining search spaces are computationally easy, and running through all possible assumptions is feasible.
$1$
s on the first column must be preserved. Any subsequent assumptions have a similar effect. For the values of n considered in this work, very few assumptions are required before complete searches through remaining search spaces are computationally easy, and running through all possible assumptions is feasible.
Assuming that Step (2) is complete, Step (3) can be implemented rather efficiently as follows. Suppose we have found a single permutation matrix Q such that
![]() $QW_{0} = X$
is symmetric. Now consider the equivalent problem of finding all P such that
$QW_{0} = X$
is symmetric. Now consider the equivalent problem of finding all P such that
![]() $PX$
is symmetric. In this case, the symmetry of
$PX$
is symmetric. In this case, the symmetry of
![]() $PX$
implies that
$PX$
implies that
It follows that
![]() $PXP = X$
, and so
$PXP = X$
, and so
![]() $(P,P^{\top })$
is a permutation automorphism of X. Since X is a symmetric
$(P,P^{\top })$
is a permutation automorphism of X. Since X is a symmetric
![]() $(0,1)$
-matrix of weight
$(0,1)$
-matrix of weight
![]() $n-k$
, it is an incidence structure. Finding the matrices P such that
$n-k$
, it is an incidence structure. Finding the matrices P such that
![]() $PXP = X$
is an incidence structure automorphism problem, for which there are efficient algorithms available in Magma [Reference Bosma, Cannon and Playoust4] that can be applied with advantage. This significantly speeds up the process of finding all of the permutation matrices P such that
$PXP = X$
is an incidence structure automorphism problem, for which there are efficient algorithms available in Magma [Reference Bosma, Cannon and Playoust4] that can be applied with advantage. This significantly speeds up the process of finding all of the permutation matrices P such that
![]() $PW_{0}$
is symmetric.
$PW_{0}$
is symmetric.
Example 5.4. The matrix
 $$ \begin{align*} W= \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & \zeta_{3} & \zeta_{3}^2 \\ 1 & 1 & 0 & \zeta_{3}^2 & \zeta_{3} \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & 1 \\ 1 & \zeta_{3}^2 & \zeta_{3} & 1 & 0 \end{bmatrix} \end{align*} $$
$$ \begin{align*} W= \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & \zeta_{3} & \zeta_{3}^2 \\ 1 & 1 & 0 & \zeta_{3}^2 & \zeta_{3} \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & 1 \\ 1 & \zeta_{3}^2 & \zeta_{3} & 1 & 0 \end{bmatrix} \end{align*} $$
is a
![]() $\mathit {CW}(5,4,3)$
that is not Hermitian (but it is symmetric). Note that
$\mathit {CW}(5,4,3)$
that is not Hermitian (but it is symmetric). Note that
![]() $W_{0} = I_{5}$
, which is already symmetric. However, W is already normalised and is not Hermitian, so we must proceed with Step (2) of the algorithm and find another permutation matrix P such that
$W_{0} = I_{5}$
, which is already symmetric. However, W is already normalised and is not Hermitian, so we must proceed with Step (2) of the algorithm and find another permutation matrix P such that
![]() $PW_{0}$
is symmetric. Any symmetric P is a candidate in this case. Let P be the permutation matrix that swaps the first two rows. Clearly, the matrix
$PW_{0}$
is symmetric. Any symmetric P is a candidate in this case. Let P be the permutation matrix that swaps the first two rows. Clearly, the matrix
![]() $PW$
is no longer normalised. Letting
$PW$
is no longer normalised. Letting
![]() $E = \mathrm {diag}(1,1,1,\zeta _{3}^{2},\zeta _{3})$
, the matrix
$E = \mathrm {diag}(1,1,1,\zeta _{3}^{2},\zeta _{3})$
, the matrix
![]() $H = PWE$
is normalised. This matrix is
$H = PWE$
is normalised. This matrix is
 $$ \begin{align*} \begin{bmatrix} 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & \zeta_{3}^{2} & \zeta_{3} \\ 1 & 1 & 0 & \zeta_{3} & \zeta_{3}^2 \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & \zeta_{3} \\ 1 & \zeta_{3}^2 & \zeta_{3} & \zeta_{3}^{2} & 0 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} \begin{bmatrix} 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & \zeta_{3}^{2} & \zeta_{3} \\ 1 & 1 & 0 & \zeta_{3} & \zeta_{3}^2 \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & \zeta_{3} \\ 1 & \zeta_{3}^2 & \zeta_{3} & \zeta_{3}^{2} & 0 \end{bmatrix}, \end{align*} $$
which is Hermitian. We can now exit the algorithm.
6 Numerical examples
Using the construction methods provided in Section 3, Table 1 presents some optimal Hermitian self-dual codes. Here,
![]() $n, k$
and q are the three parameters of the complex weighing matrices, and the parameters of the codes are
$n, k$
and q are the three parameters of the complex weighing matrices, and the parameters of the codes are
![]() $[2n,n,d].$
$[2n,n,d].$
Table 1 Optimal Hermitian self-dual codes.

Definition 6.1. The direct sum of an n-order square matrix and an m-order square matrix is defined as
 $$ \begin{align*} A\oplus B=\begin{bmatrix} A & 0_{n\times m}\\ 0_{m\times n} & B \end{bmatrix}. \end{align*} $$
$$ \begin{align*} A\oplus B=\begin{bmatrix} A & 0_{n\times m}\\ 0_{m\times n} & B \end{bmatrix}. \end{align*} $$
Remark 6.2. Among the codes presented in Table 1, the three codes with parameters
![]() $[12,6,4]$
are nonequivalent, as well as the two codes with parameters
$[12,6,4]$
are nonequivalent, as well as the two codes with parameters
![]() $[16,8,6].$
$[16,8,6].$
Remark 6.3. The three matrices
![]() $W_1 \in \mathit {CW}(5,4,3)$
,
$W_1 \in \mathit {CW}(5,4,3)$
,
![]() $W_2 \in \mathit {CW}(6,4,6)$
and
$W_2 \in \mathit {CW}(6,4,6)$
and
![]() $W_3 \in \mathit {CW}(12,6,3)$
in Table 1 are derived as equivalent Hermitian matrices using the algorithm in Section 5 and are subsequently used to construct Hermitian self-dual codes via Theorem 3.2. The Hermitian matrix for
$W_3 \in \mathit {CW}(12,6,3)$
in Table 1 are derived as equivalent Hermitian matrices using the algorithm in Section 5 and are subsequently used to construct Hermitian self-dual codes via Theorem 3.2. The Hermitian matrix for
![]() $W_1$
is provided in Example 5.4, while the Hermitian matrices
$W_1$
is provided in Example 5.4, while the Hermitian matrices
![]() $W_2'$
for
$W_2'$
for
![]() $W_2$
and
$W_2$
and
![]() $W_3'$
for
$W_3'$
for
![]() $W_3$
are presented in the Appendix. The remaining matrices can be directly used to construct Hermitian self-dual codes via Theorem 3.1.
$W_3$
are presented in the Appendix. The remaining matrices can be directly used to construct Hermitian self-dual codes via Theorem 3.1.
Appendix
 $$ \begin{align*} W_2'= \left[\begin{array}{cccccc} 1 & 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 0 & 1 & \zeta_{3}^2 & \zeta_3 \\ 0 & 0 & 1 & 1 & \zeta_{3} & \zeta_{3}^2\\ 1 & 1 & 1 & -1 & 0 & 0 \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & -1 & 0 \\ 1 & \zeta_3^2 & \zeta_3 & 0 & 0 & -1 \end{array}\right], \end{align*} $$
$$ \begin{align*} W_2'= \left[\begin{array}{cccccc} 1 & 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 0 & 1 & \zeta_{3}^2 & \zeta_3 \\ 0 & 0 & 1 & 1 & \zeta_{3} & \zeta_{3}^2\\ 1 & 1 & 1 & -1 & 0 & 0 \\ 1 & \zeta_{3} & \zeta_{3}^2 & 0 & -1 & 0 \\ 1 & \zeta_3^2 & \zeta_3 & 0 & 0 & -1 \end{array}\right], \end{align*} $$
 $$ \begin{align*} W_3'= \left[\begin{array}{cccccccccccc} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 \\ 1 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & 1 & 0 \\ 0 & 1 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 &\zeta_3^2 \\ 1 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 \\ 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & 1 \\ 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 \\ 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3 \\ 1 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0\\ 0 & 1 & 0 & 1 & 0 & \zeta_3 & 0 &\zeta_3^2 & 0 & \zeta_3^2 & 0 & \zeta_3 \\ 1 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 \end{array}\right]. \end{align*} $$
$$ \begin{align*} W_3'= \left[\begin{array}{cccccccccccc} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 \\ 1 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & 1 & 0 \\ 0 & 1 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 &\zeta_3^2 \\ 1 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 \\ 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & 1 \\ 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 \\ 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 & 1 & 0 & \zeta_3 & 0 & \zeta_3 \\ 1 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0 & \zeta_3^2 & 0 & \zeta_3 & 0\\ 0 & 1 & 0 & 1 & 0 & \zeta_3 & 0 &\zeta_3^2 & 0 & \zeta_3^2 & 0 & \zeta_3 \\ 1 & 0 & \zeta_3 & 0 & \zeta_3 & 0 & 1 & 0 & \zeta_3^2 & 0 & \zeta_3^2 & 0 \end{array}\right]. \end{align*} $$