Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Anderssen, R. S.
and
Loy, R. J.
2002.
Rheological implications of completely monotone fading memory.
Journal of Rheology,
Vol. 46,
Issue. 6,
p.
1459.
Husain, Saiful A.
and
Anderssen, R.S.
2005.
Modelling the relaxation modulus of linear viscoelasticity using Kohlrausch functions.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 125,
Issue. 2-3,
p.
159.
Anderssen, R. S.
Davies, A. R.
and
de Hoog, F. R.
2008.
On the sensitivity of interconversion between relaxation and creep.
Rheologica Acta,
Vol. 47,
Issue. 2,
p.
159.
Nobile, Maria Rossella
and
Cocchini, Franco
2008.
A generalized relation between MWD and relaxation time spectrum.
Rheologica Acta,
Vol. 47,
Issue. 5-6,
p.
509.
Friedrich, Christian
Loy, Richard J.
and
Anderssen, Robert S.
2009.
Relaxation time spectrum molecular weight distribution relationships.
Rheologica Acta,
Vol. 48,
Issue. 2,
p.
151.
Seredyńska, M.
and
Hanyga, Andrzej
2010.
Relaxation, dispersion, attenuation, and finite propagation speed in viscoelastic media.
Journal of Mathematical Physics,
Vol. 51,
Issue. 9,
Hanyga, A.
2014.
Dispersion and Attenuation for an Acoustic Wave Equation Consistent with Viscoelasticity.
Journal of Computational Acoustics,
Vol. 22,
Issue. 03,
p.
1450006.
Li, Jun-jie
Cheng, Xuan
Zhang, Ying
and
Sun, Wei-xiang
2016.
A revisit of strain-rate frequency superposition of dense colloidal suspensions under oscillatory shears.
Journal of Central South University,
Vol. 23,
Issue. 8,
p.
1873.
Hanyga, Andrzej
2016.
Wave Propagation in Anisotropic Viscoelasticity.
Journal of Elasticity,
Vol. 122,
Issue. 2,
p.
231.
Minakov, Alexander A.
and
Schick, Christoph
2018.
Nanometer scale thermal response of polymers to fast thermal perturbations.
The Journal of Chemical Physics,
Vol. 149,
Issue. 7,
Minakov, Alexander A.
and
Schick, Christoph
2018.
Non-equilibrium fast thermal response of polymers.
Thermochimica Acta,
Vol. 660,
Issue. ,
p.
82.
Minakov, Alexander A.
and
Schick, Christoph
2019.
Nanoscale Heat Conduction in CNT-POLYMER Nanocomposites at Fast Thermal Perturbations.
Molecules,
Vol. 24,
Issue. 15,
p.
2794.
Górska, K.
and
Horzela, A.
2020.
The Volterra type equations related to the non-Debye relaxation.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 85,
Issue. ,
p.
105246.
Górska, Katarzyna
and
Horzela, Andrzej
2021.
Non-Debye Relaxations: Two Types of Memories and Their Stieltjes Character.
Mathematics,
Vol. 9,
Issue. 5,
p.
477.
Górska, K.
Horzela, A.
and
Pogány, T.K.
2021.
Non-Debye relaxations: The characteristic exponent in the excess wings model.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 103,
Issue. ,
p.
106006.
Minakov, Alexander A.
and
Schick, Christoph
2021.
Integro-Differential Equation for the Non-Equilibrium Thermal Response of Glass-Forming Materials: Analytical Solutions.
Symmetry,
Vol. 13,
Issue. 2,
p.
256.
Górska, Katarzyna
and
Horzela, Andrzej
2023.
Subordination and memory dependent kinetics in diffusion and relaxation phenomena.
Fractional Calculus and Applied Analysis,
Vol. 26,
Issue. 2,
p.
480.
Górska, K
Horzela, A
and
Penson, K A
2023.
The Havriliak–Negami and Jurlewicz–Weron–Stanislavsky relaxation models revisited: memory functions based study.
Journal of Physics A: Mathematical and Theoretical,
Vol. 56,
Issue. 31,
p.
313001.
 which defines how the stress σ(t) at time t depends on the earlier history of the shear rate
which defines how the stress σ(t) at time t depends on the earlier history of the shear rate 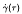 via the relaxation modulus (kernel) G (t). Physical reality is achieved by requiring that the form of the relaxation modulus G (t) gives the Boltzmann equation fading memory, so that changes in the distant past have less effect now than the same changes in the more recent past. A popular choice, though others have previously been proposed and investigated, is the assumption that G (t) be a completely monotone function. This assumption has much deeper ramifications than have been identified, discussed or exploited in the rheological literature. The purpose of this paper is to review the key mathematical properties of completely monotone functions, and to illustrate how these properties impact on the theory and application of linear viscoelasticity and polymer dynamics. A more general representation of a completely monotone function, known in the mathematical literature, but not the rheological, is formulated and discussed. This representation is used to derive new rheological relationships. In particular, explicit inversion formulas are derived for the relationships that are obtained when the relaxation spectrum model and a mixing rule are linked through a common relaxation modulus.
via the relaxation modulus (kernel) G (t). Physical reality is achieved by requiring that the form of the relaxation modulus G (t) gives the Boltzmann equation fading memory, so that changes in the distant past have less effect now than the same changes in the more recent past. A popular choice, though others have previously been proposed and investigated, is the assumption that G (t) be a completely monotone function. This assumption has much deeper ramifications than have been identified, discussed or exploited in the rheological literature. The purpose of this paper is to review the key mathematical properties of completely monotone functions, and to illustrate how these properties impact on the theory and application of linear viscoelasticity and polymer dynamics. A more general representation of a completely monotone function, known in the mathematical literature, but not the rheological, is formulated and discussed. This representation is used to derive new rheological relationships. In particular, explicit inversion formulas are derived for the relationships that are obtained when the relaxation spectrum model and a mixing rule are linked through a common relaxation modulus.

