Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-27T02:46:14.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely continuous elements of Banach algebras related to locally compact groups

Published online by Cambridge University Press:  17 April 2009

M. J. Mehdipour  and
R. Nasr-Isfahani
M. J. Mehdipour
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156–83111, Iran, e-mail: [email protected]
R. Nasr-Isfahani
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156–83111, Iran, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

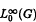Let G be a locally compact group and be the Banach space of all essentially bounded measurable functions on 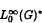G vansihing an infinity. Here, we study some families of right completely continuous elements in the Banach algebra equipped with an Arens type product. As the main result, we show that has a certain right completely continuous element if and only if G is compact.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 76 , Issue 1 , August 2007 , pp. 49 - 54
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Akemann, C.A., ‘Some mapping properties of the group algebras of a compact group’, Pacific J. Math. 22 (1967), 1–8.CrossRefGoogle Scholar
[2]Ghahramani, F., Lau, A.T. and Losert, V., ‘Isometric isomorphisms between Banach algebras related to locally compact groups’, Trans. Amer. Math. Soc. 321 (1990), 273–283.CrossRefGoogle Scholar
[3]Ghahramani, F. and Lau, A.T., ‘Isomorphisms and multipliers on second dual algebras of Banach algebras’, Math. Proc. Cambridge Philos. Soc. 111 (1992), 161–168.CrossRefGoogle Scholar
[4]Ghahramani, F. and Lau, A.T., ‘Multipliers and ideal in second conjugate algebras related to locally compact groups’, J. Funct. Anal. 132 (1995), 170–191.CrossRefGoogle Scholar
[5]Ghahramani, F. and Lau, A.t., ‘Multipliers ad modulus on Banach algebras related to locally compact groups’, J. Funct. Anal 150 (1997), 478–497.CrossRefGoogle Scholar
[6]Hewitt, E. and Ross, K., Abstract harmonic analysis I (Springer-Verlag, New York, 1970).Google Scholar
[7]Hewitt, E. and Stromberg, K., Real and abstract analysis (Springer-Verlag, New York, 1995).Google Scholar
[8]Isik, N., Pym, J. and Ülger, A., ‘The second dual of the group algebra of a compact group’, J. London Math. Soc. 35 (1987), 135–148.CrossRefGoogle Scholar
[9]Lau, A.T. and Pym, J., ‘Concerning the second dual of the group algebra of a locally compact group’, J. London Math. Soc. 41 (1990), 445–460.CrossRefGoogle Scholar
[10]Lau, A.T. and Ülger, A., ‘Topological centers of certain dual algebras’, Trans. Amer. Math. Soc. 348 (1996), 1191–1212.CrossRefGoogle Scholar
[11]Losert, V., ‘Weakly compact multipliers on group algebras’, J. Funct. Anal. 213 (2004), 466–472.CrossRefGoogle Scholar
[12]Sakai, S., ‘Weakly compact operators on operator algebras’, Pacific J. Math 14 (1964), 659–664.CrossRefGoogle Scholar