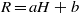Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Araújo, Jogli Gidel da Silva
de Lima, Henrique Fernandes
dos Santos, Fábio Reis
and
Velásquez, Marco Antonio Lázaro
2019.
Complete linear Weingarten spacelike submanifolds with higher codimension in the de Sitter space.
International Journal of Geometric Methods in Modern Physics,
Vol. 16,
Issue. 04,
p.
1950050.
de Lima, Eudes L.
and
de Lima, Henrique F.
2021.
Characterizing closed linear Weingarten spacelike submanifolds immersed in the de Sitter space.
São Paulo Journal of Mathematical Sciences,
Vol. 15,
Issue. 1,
p.
322.
Barboza, Weiller F. C.
de Lima, Eudes L.
de Lima, Henrique F.
and
Velásquez, Marco Antonio L.
2022.
On the umbilicity of linear Weingarten spacelike submanifolds immersed in the de Sitter space.
Bulletin of Mathematical Sciences,
Vol. 12,
Issue. 02,
Antonia, Railane
and
de Lima, Henrique F.
2022.
On the parabolicity of linear Weingarten spacelike submanifolds in the de Sitter space.
Quaestiones Mathematicae,
Vol. 45,
Issue. 10,
p.
1589.
de Lima, Henrique F.
Rocha, Lucas S.
and
Velásquez, Marco Antonio L.
2023.
Rigidity of spacelike LW-submanifolds in the de Sitter space.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 72,
Issue. 4,
p.
2389.