Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-27T02:29:43.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete spacelike hypersurfaces in a de Sitter space

Published online by Cambridge University Press:  17 April 2009

Shu Shichang
Shu Shichang
Affiliation:
Department of Mathematics, Xianyang Teachers' University, Xianyang 712000, Shaanxi, Peoples Republic of China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

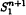In this paper, we characterise the n-dimensional (n ≥ 3) complete spacelike hypersurfaces Mn in a de Sitter space with constant scalar curvature and with two distinct principal curvatures. We show that if the multiplicities of such principal curvatures are greater than 1, then Mn is isometric to Hk (sinh r) × Sn−k (cosh r), 1 < k < n − 1. In particular, when Mn is the complete spacelike hypersurfaces in 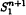with the scalar curvature and the mean curvature being linearly related, we also obtain a characteristic Theorem of such hypersurfaces.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 1 , February 2006 , pp. 9 - 16
Copyright
Copyright © Australian Mathematical Society 2006

References

Referenes

[1]Abe, N., Koike, N. and Yamaguchi, S., ‘Congruence theorems for proper semi-Riemannian hypersurfaces in a real space form’, Yokohama Math. J. 35 (1987), 123–136.Google Scholar
[2]Akutagawa, K., ‘On spacelike hypersurfaces with constant mean curvature in a de Sitter space’, Math. Z. 196 (1987), 13–19.CrossRefGoogle Scholar
[3]Alencar, H. and do Carmo, M.P., ‘Hypersurfaces with constant mean curvature in spheres’, Proc. Amer. Math. Soc. 120 (1994), 1223–1229.CrossRefGoogle Scholar
[4]Cheng, Q.M., ‘Complete spacelike hypersurfaces of a de Sitter space with r = kH’, Mem. Fac. Sci. Kyushu Univ. 44 (1990), 67–77.Google Scholar
[5]Cheng, S.Y. and Yau, S.T., ‘Hypersurfaces with constant scalar curvature’, Math. Ann. 225 (1977), 195–204.CrossRefGoogle Scholar
[6]Goddard, A.J., ‘Some remarks on the existence of spacelike hypersurfaces of constant mean curvature’, Math. Proc. Cambridge Phil. Soc. 82 (1977), 489–495.CrossRefGoogle Scholar
[7]A.B., Jr, Colares, A.G. and Palmas, O., ‘Complete spacelike hypersurfaces with constant mean curvature in the de Sitter space: A gap Theorem’, Illinois J. Maths. 47 (2003), 847–866.Google Scholar
[8]Liu, X., ‘Complete spacelike hypersurfaces with constant scalar curvature’, Manuscripta Math. 105 (2001), 367–377.CrossRefGoogle Scholar
[9]Montiel, S., ‘A characterization of hyperbolic cylinders in the de Sitter space’, Tôhoku Math. J. 48 (1996), 23–31.CrossRefGoogle Scholar
[10]Nomizu, K., ‘On isoparametric hypersurfaces in the Lorentzian space forms’, Japan. J. Math. 7 (1981), 217–226.CrossRefGoogle Scholar
[11]Okumura, M., ‘Hypersurfaces and a pinching problem on the second fundamental tensor’, Amer. J.Math. 96 (1974), 207–213.CrossRefGoogle Scholar
[12]Otsuki, T., ‘Minimal hypersurfaces in a Riemannian manifold of constant curvature’, Amer. J.Math. 92 (1970), 145–173.CrossRefGoogle Scholar
[13]Ramanathan, J., ‘Complete spacelike hypersurfaces of constant mean curvature in the de Sitter space’, Indiana University Math. J. 36 (1987), 349–359.CrossRefGoogle Scholar
[14]Zheng, Y., ‘Spacelike hypersurfaces with constant scalar curvature in the de Sitter spaces’, Differential Geom. Appl. 6 (1996), 51–54.Google Scholar
[15]Zheng, Y., ‘On spacelike hypersurfaces in the de Sitter spaces’, Ann. Global Anal. Geom. 13 (1995), 317–321.CrossRefGoogle Scholar