A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS

Abstract

Let 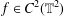$f\in C^{2}(\mathbb{T}^{2})$ have mean value 0 and consider

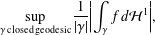$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D6FE}\,\text{closed geodesic}}\frac{1}{|\unicode[STIX]{x1D6FE}|}\biggl|\int _{\unicode[STIX]{x1D6FE}}f\,d{\mathcal{H}}^{1}\biggr|,\end{eqnarray}$$

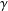where $\unicode[STIX]{x1D6FE}$ ranges over all closed geodesics 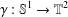$\unicode[STIX]{x1D6FE}:\mathbb{S}^{1}\rightarrow \mathbb{T}^{2}$ and 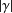$|\unicode[STIX]{x1D6FE}|$ denotes its length. We prove that this supremum is always attained. Moreover, we can bound the length of the geodesic 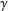$\unicode[STIX]{x1D6FE}$ attaining the supremum in terms of the smoothness of the function: for all 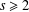$s\geq 2$,

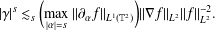$$\begin{eqnarray}|\unicode[STIX]{x1D6FE}|^{s}{\lesssim}_{s}\biggl(\max _{|\unicode[STIX]{x1D6FC}|=s}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{1}(\mathbb{T}^{2})}\biggr)\Vert \unicode[STIX]{x1D6FB}f\Vert _{L^{2}}\Vert f\Vert _{L^{2}}^{-2}.\end{eqnarray}$$