Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
NATH, RAJAT KANTI
2013.
COMMUTATIVITY DEGREE OF A CLASS OF FINITE GROUPS AND CONSEQUENCES.
Bulletin of the Australian Mathematical Society,
Vol. 88,
Issue. 3,
p.
448.
Russo, Francesco G.
2016.
Strong subgroup commutativity degree and some recent problems on the commuting probabilities of elements and subgroups.
Quaestiones Mathematicae,
Vol. 39,
Issue. 8,
p.
1019.
Dutta, Jutirekha
2016.
On a Problem Posed by Belcastro and Sherman.
Kyungpook mathematical journal,
Vol. 56,
Issue. 1,
p.
121.
Nath, Rajat Kanti
2019.
On asymptotic commutativity degree of finite groups.
Proyecciones (Antofagasta),
Vol. 38,
Issue. 4,
p.
829.
Farrokhi D. G., M.
2022.
Finite Groups with Five Relative Commutativity Degrees.
Results in Mathematics,
Vol. 77,
Issue. 2,
Dutta, Jutirekha
Basnet, Dhiren Kumar
and
Nath, Rajat Kanti
2023.
Characterization and commuting probability of n-centralizer finite rings.
Proyecciones (Antofagasta),
Vol. 42,
Issue. 6,
p.
1489.


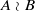 of finite Abelian groups
of finite Abelian groups 